 We continue to live through incredibly turbulent times. In the past decade or so we have experienced a global financial crisis, a global health emergency, seen the UK’s departure from the European Union, and witnessed increasing levels of geopolitical tension and conflict. Add to this the effects from the climate emergency and it easy to see why the issue of economic uncertainty is so important when thinking about a country’s economic prospects.
We continue to live through incredibly turbulent times. In the past decade or so we have experienced a global financial crisis, a global health emergency, seen the UK’s departure from the European Union, and witnessed increasing levels of geopolitical tension and conflict. Add to this the effects from the climate emergency and it easy to see why the issue of economic uncertainty is so important when thinking about a country’s economic prospects.
In this blog we consider how we can capture this uncertainty through a World Uncertainty Index and the ways by which economic uncertainty impacts on the macroeconomic environment.
World Uncertainty Index
Hites Ahir, Nicholas Bloom and Davide Furceri have constructed a measure of uncertainty known as the World Uncertainty Index (WUI). This tracks uncertainty around the world using the process of ‘text mining’ the country reports produced by the Economist Intelligence Unit. The words searched for are ‘uncertain’, ‘uncertainty’ and ‘uncertainties’ and a tally is recorded based on the number of times they occur per 1000 words of text. To produce the index this figure is then multiplied up by 100 000. A higher number therefore indicates a greater level of uncertainty. For more information on the construction of the index see the 2022 article by Ahir, Bloom and Furceri linked below.
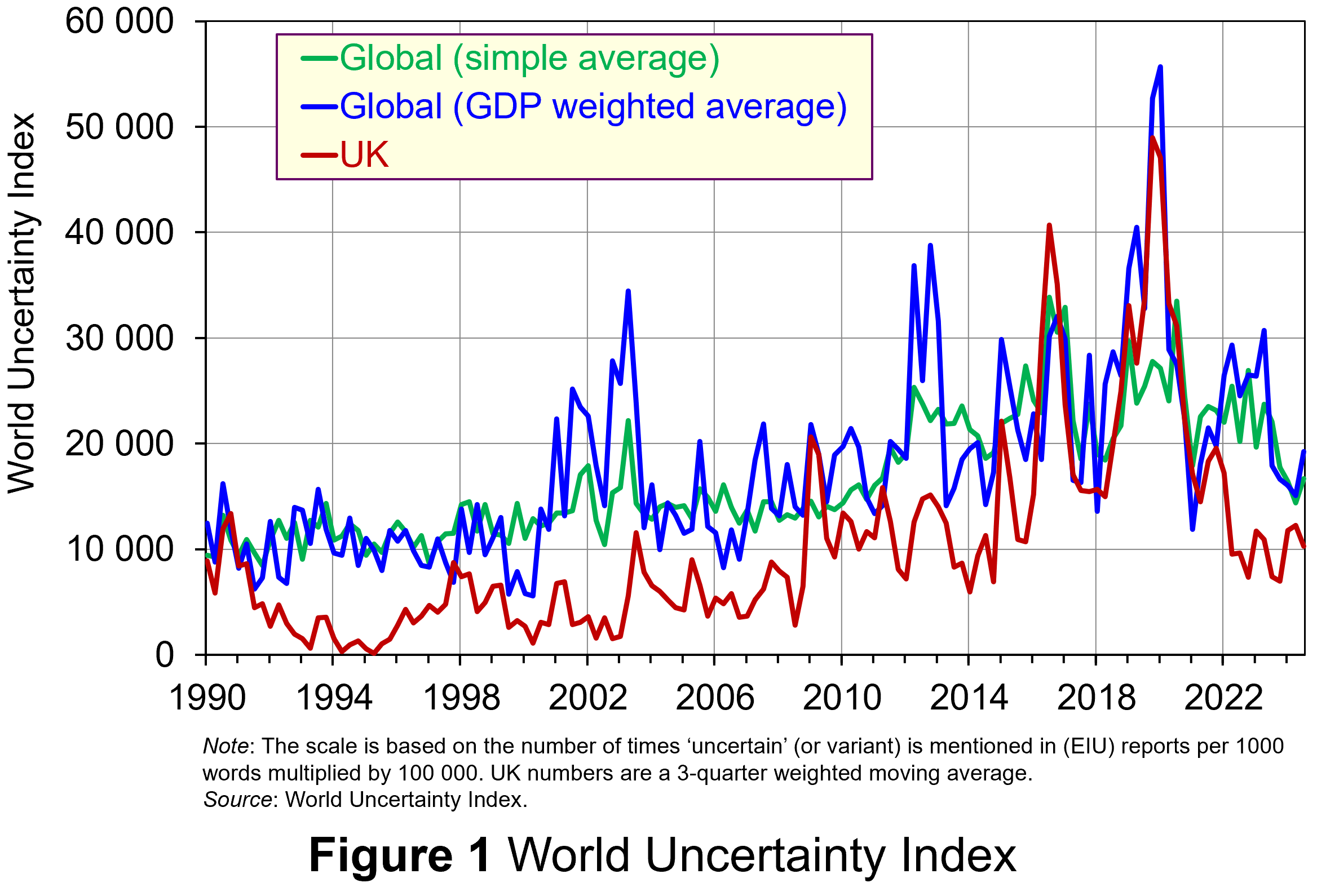 Figure 1 (click here for a PowerPoint) shows the WUI both globally and in the UK quarterly since 1991. The global index covers 143 countries and is presented as both a simple average and a GDP weighted average. The UK WUI is also shown. This is a three-quarter weighted average, the authors’ preferred measure for individual countries, where increasing weights of 0.1, 0.3 and 0.6 are used for the three most recent quarters.
Figure 1 (click here for a PowerPoint) shows the WUI both globally and in the UK quarterly since 1991. The global index covers 143 countries and is presented as both a simple average and a GDP weighted average. The UK WUI is also shown. This is a three-quarter weighted average, the authors’ preferred measure for individual countries, where increasing weights of 0.1, 0.3 and 0.6 are used for the three most recent quarters.
From Figure 1 we can see how the level of uncertainty has been particularly volatile over the past decade or more. Events such as the sovereign debt crisis in parts of Europe in the early 2010s, the Brexit referendum in 2016, the COVID-pandemic in 2020–21 and the invasion of Ukraine in 2022 all played their part in affecting uncertainty domestically and internationally.
Uncertainty, risk-aversion and aggregate demand
Now the question turns to how uncertainty affects economies. One way of addressing this is to think about ways in which uncertainty affects the choices that people and businesses make. In doing so, we could think about the impact of uncertainty on components of aggregate demand, such as household consumption and investment, or capital expenditures by firms.
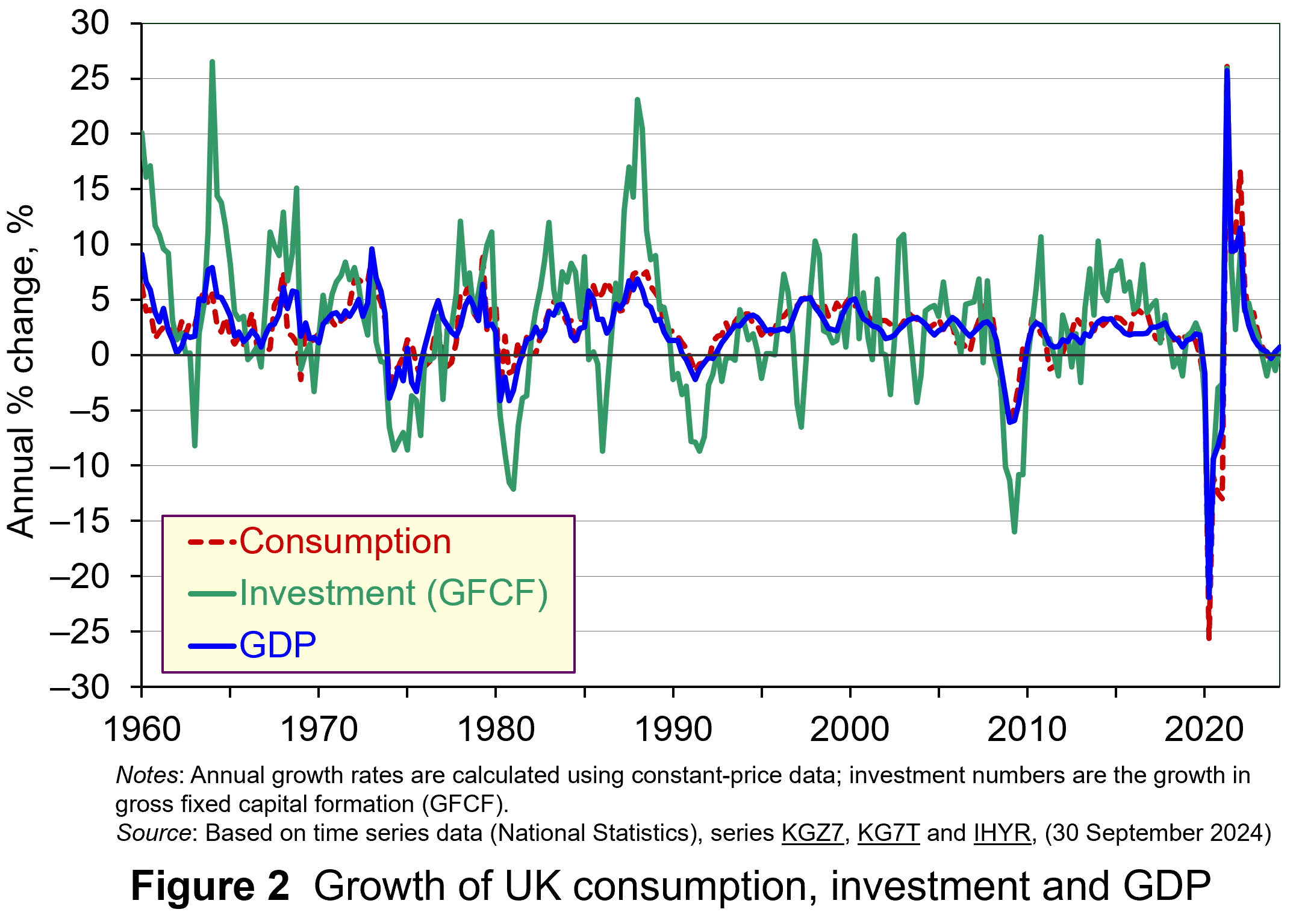 As Figure 2 shows (click here for a PowerPoint), investment is particularly volatile, and much more so than household spending. Some of this can be attributed to the ‘lumpiness’ of investment decisions since these expenditures tend to be characterised by indivisibility and irreversibility. This means that they are often relatively costly to finance and are ‘all or nothing’ decisions. In the context of uncertainty, it can make sense therefore for firms to wait for news that makes the future clearer. In this sense, we can think of uncertainty rather like a fog that firms are peering through. The thicker the fog, the more uncertain the future and the more cautious firms are likely to be.
As Figure 2 shows (click here for a PowerPoint), investment is particularly volatile, and much more so than household spending. Some of this can be attributed to the ‘lumpiness’ of investment decisions since these expenditures tend to be characterised by indivisibility and irreversibility. This means that they are often relatively costly to finance and are ‘all or nothing’ decisions. In the context of uncertainty, it can make sense therefore for firms to wait for news that makes the future clearer. In this sense, we can think of uncertainty rather like a fog that firms are peering through. The thicker the fog, the more uncertain the future and the more cautious firms are likely to be.
The greater caution that many firms are likely to adopt in more uncertain times is consistent with the property of risk-aversion that we often attribute to a range of economic agents. When applied to household spending decisions, risk-aversion is often used to explain why households are willing to hold a buffer stock of savings to self-insure against unforeseen events and their future financial outcomes being worse than expected. Hence, in more uncertain times households are likely to want to increase this buffer further.
 The theory of buffer-stock saving was popularised by Christopher Carroll in 1992 (see link below). It implies that in the presence of uncertainty, people are prepared to consume less today in order to increase levels of saving, pay off existing debts, or borrow less relative to that in the absence of uncertainty. The extent of the buffer of financial wealth that people want to hold will depend on their own appetite for risk, the level of uncertainty, and the moderating effect from their own impatience and, hence, present bias for consuming today.
The theory of buffer-stock saving was popularised by Christopher Carroll in 1992 (see link below). It implies that in the presence of uncertainty, people are prepared to consume less today in order to increase levels of saving, pay off existing debts, or borrow less relative to that in the absence of uncertainty. The extent of the buffer of financial wealth that people want to hold will depend on their own appetite for risk, the level of uncertainty, and the moderating effect from their own impatience and, hence, present bias for consuming today.
Risk aversion is consistent with the property of diminishing marginal utility of income or consumption. In other words, as people’s total spending volumes increase, their levels of utility or satisfaction increase but at an increasingly slower rate. It is this which explains why individuals are willing to engage with the financial system to reallocate their expected life-time earnings and have a smoother consumption profile than would otherwise be the case from their fluctuating incomes.
Yet diminishing marginal utility not only explains consumption smoothing, but also why people are willing to engage with the financial system to have financial buffers as self-insurance. It explains why people save more or borrow less today than suggested by our base-line consumption smoothing model. It is the result of people’s greater dislike (and loss of utility) from their financial affairs being worse than expected than their like (and additional utility) from them being better than expected. This tendency is only likely to increase the more uncertain times are. The result is that uncertainty tends to lower household consumption with perhaps ‘big-ticket items’, such as cars, furniture, and expensive electronic goods, being particularly sensitive to uncertainty.
Uncertainty and confidence
Uncertainty does not just affect risk; it also affects confidence. Risk and confidence are often considered together, not least because their effects in generating and transmitting shocks can be difficult to disentangle.
We can think of confidence as capturing our mood or sentiment, particularly with respect to future economic developments. Figure 3 plots the Uncertainty Index for the UK alongside the OECD’s composite consumer and business confidence indicators. Values above 100 for the confidence indicators indicate greater confidence about the future economic situation and near-term business environment, while values below 100 indicate pessimism towards the future economic and business environments.
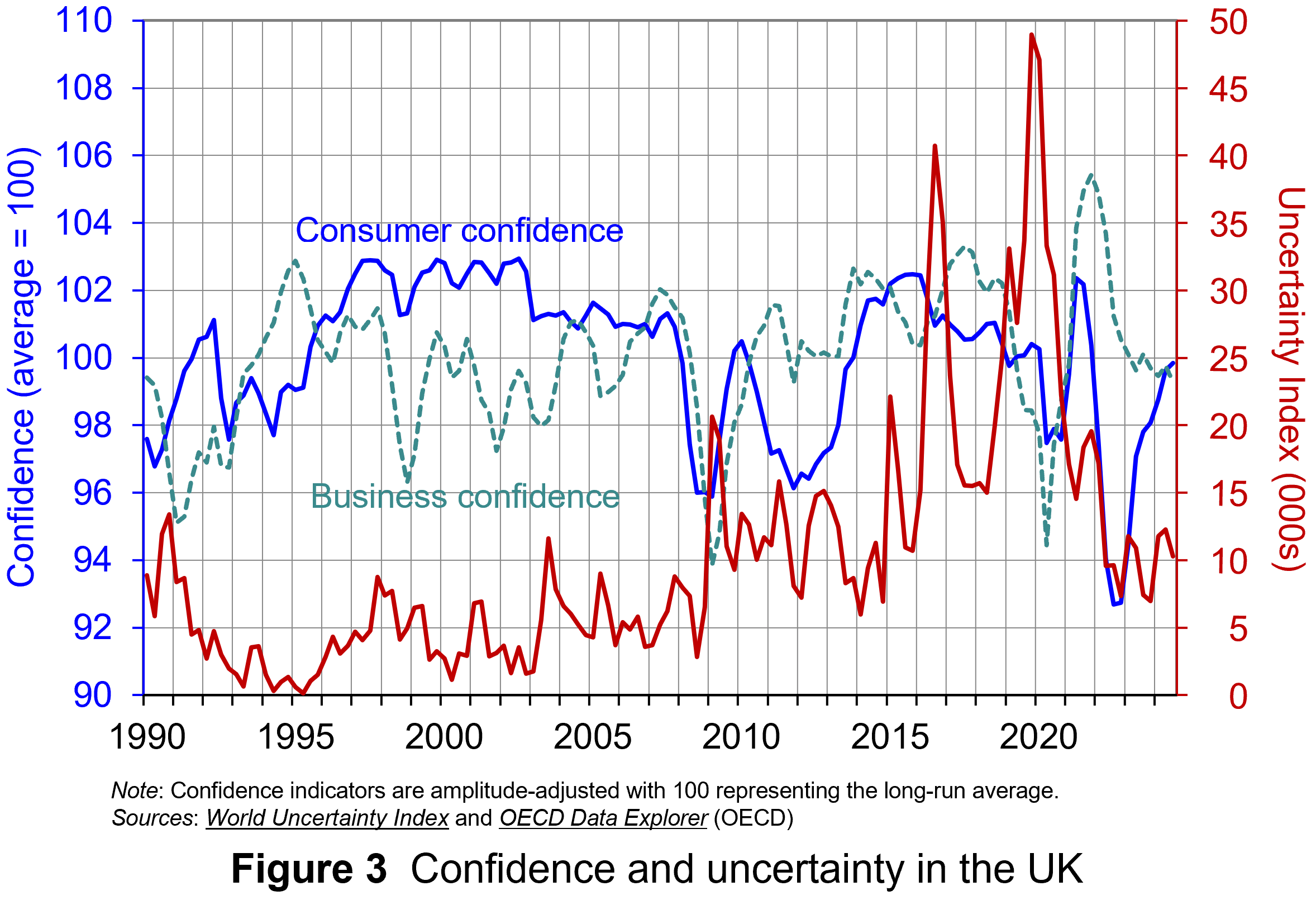 Figure 3 suggests that the relationship between confidence and uncertainty is rather more complex than perhaps is generally understood (click here for a PowerPoint). Haddow, Hare, Hooley and Shakir (see link below) argue that the evidence tends to point to changes in uncertainty affecting confidence, but with less evidence that changes in confidence affect uncertainty.
Figure 3 suggests that the relationship between confidence and uncertainty is rather more complex than perhaps is generally understood (click here for a PowerPoint). Haddow, Hare, Hooley and Shakir (see link below) argue that the evidence tends to point to changes in uncertainty affecting confidence, but with less evidence that changes in confidence affect uncertainty.
To illustrate this, consider the global financial crisis of the late 2000s. The argument can be made that the heightened uncertainty about future prospects for households and businesses helped to erode their confidence in the future. The result was that people and businesses revised down their expectations of the future (pessimism). However, although people were more pessimistic about the future, this was more likely to have been the result of uncertainty rather than the cause of further uncertainty.
Conclusion
For economists and policymakers alike, indicators of uncertainty, such as the Ahir, Bloom and Furceri World Uncertainty Index, are invaluable tools in understanding and forecasting behaviour and the likely economic outcomes that follow. Some uncertainty is inevitable, but the persistence of greater uncertainty since the global financial crisis of the late 2000s compares quite starkly with the relatively lower and more stable levels of uncertainty seen from the mid-1990s up to the crisis. Hence the recent frequency and size of changes in uncertainty show how important it to understand how uncertainty effects transmit through economies.
Academic papers
- The World Uncertainty Index
National Bureau of Economic Research, Working Paper 29763, Hites Ahir, Nicholas Bloom and Davide Furceri (February 2022)
- The Buffer-Stock Theory of Saving: Some Macroeconomic Evidence
Brookings Papers on Economic Activity, Christopher D Carroll (Vol 2, 1992)
- Macroeconomic uncertainty: what is it, how can we measure it and why does it matter?
Bank of England Quarterly Bulletin, 2013 Q2, Abigail Haddow, Chris Hare, John Hooley and Tamarah Shakir (13/6/13)
Articles
Data
Questions
- (a) Explain what is meant by the concept of diminishing marginal utility of consumption.
(b) Explain how this concept helps us to understand both consumption smoothing and the motivation to engage in buffer-stock saving.
- Explain the distinction between confidence and uncertainty when analysing macroeconomic shocks.
- Discuss which types of expenditures you think are likely to be most susceptible to uncertainty shocks.
- Discuss how economic uncertainty might affect productivity and the growth of potential output.
- How might the interconnectedness of economies affect the transmission of uncertainty effects through economies?
 A common practice of international investors is to take part in the so-called ‘carry trade’. This involves taking advantage of nominal interest rate differences between countries. For example, assume that interest rates are low in Japan and high in the USA. It is thus profitable to borrow yen in Japan at the low interest rate, exchange it into US dollars and deposit the money at the higher interest rate available in the USA. If there is no change in the exchange rate between the dollar and the yen, the investor makes a profit equal to the difference in the interest rates.
A common practice of international investors is to take part in the so-called ‘carry trade’. This involves taking advantage of nominal interest rate differences between countries. For example, assume that interest rates are low in Japan and high in the USA. It is thus profitable to borrow yen in Japan at the low interest rate, exchange it into US dollars and deposit the money at the higher interest rate available in the USA. If there is no change in the exchange rate between the dollar and the yen, the investor makes a profit equal to the difference in the interest rates.
Rather than depositing the money in a US bank account, an alternative is to purchase US bonds or other assets in the USA, where the return is again higher than that in Japan.
If, however, interest-rate differentials narrow, there is the possibility of the carry trade ‘unwinding’. Not only may the carry trade prove unprofitable (or less so), but investors may withdraw their deposits and pay back the loans. This, as we shall, can have adverse consequences on exchange rates.
The problem of an unwinding of the carry trade is not new. It worsened the underlying problems of the financial crisis in 2008. The question today is whether history is about to repeat itself with a new round of unwinding of the carry trade threatening economic growth and recovery around the world.
We start by looking at what happened in 2008.
The carry trade and the 2008 financial crisis
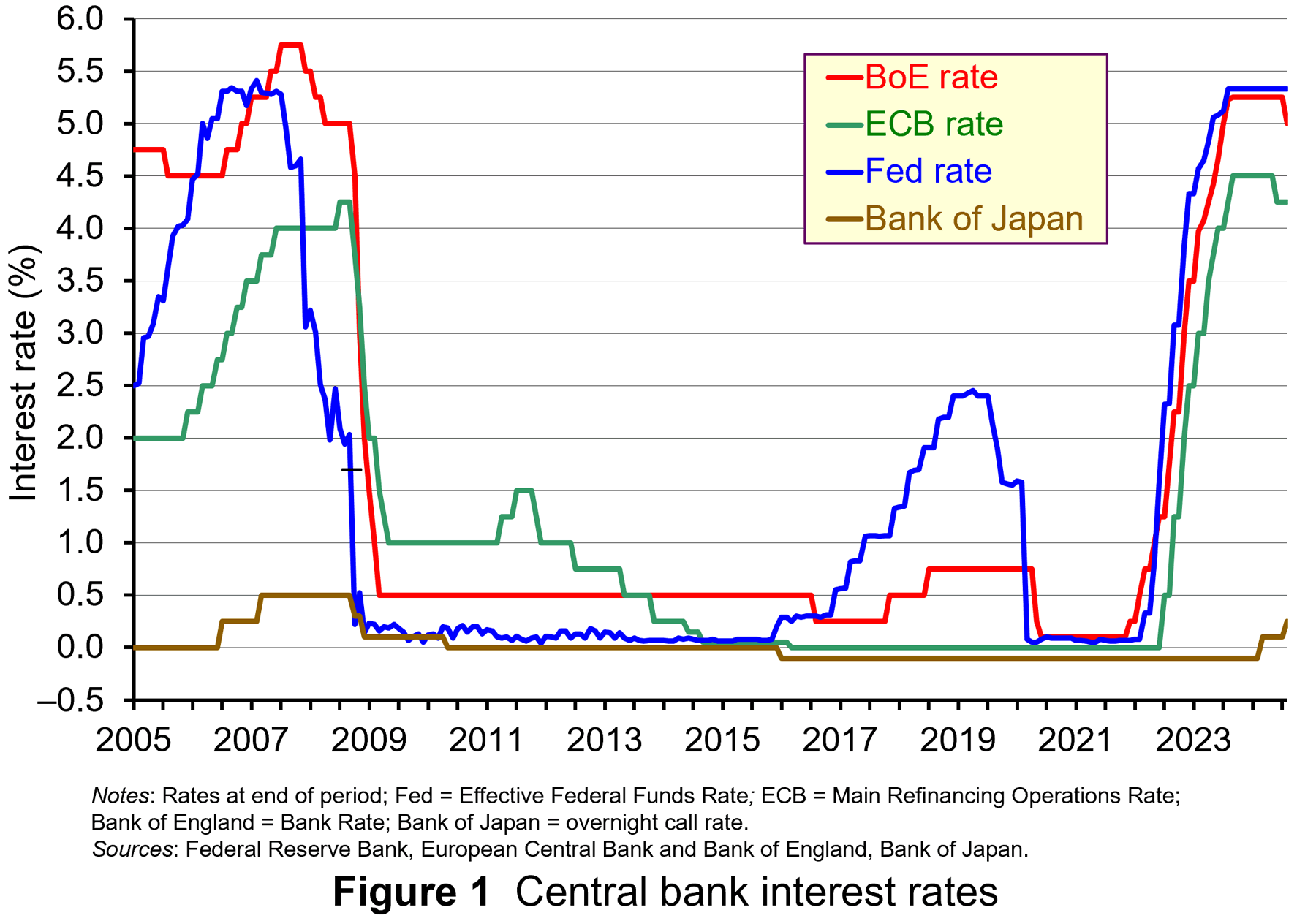 Prior to the financial crisis of 2008, current account deficit countries, such as the UK, USA and Australia, typically had relatively high interest rates, while current account surplus countries such as Japan and Switzerland had relatively low ones. Figure 1 shows central bank interest rates from 2005 to the current day (click here for a PowerPoint).
Prior to the financial crisis of 2008, current account deficit countries, such as the UK, USA and Australia, typically had relatively high interest rates, while current account surplus countries such as Japan and Switzerland had relatively low ones. Figure 1 shows central bank interest rates from 2005 to the current day (click here for a PowerPoint).
The carry trade saw investors borrowing money in Japan and Switzerland, exchanging it on the foreign exchange market, with the currency then deposited in the UK, USA and Australia. Hundreds of billions worth of dollars were involved in this carry trade.
If, however, the higher interest rates in the UK and other deficit countries were simply to compensate investors for the risk of currency depreciation, then there would be no excessive inflow of finance. The benefit of the higher interest rate would be offset by a depreciating currency. But the carry trade had the effect of making deficit currencies appreciate, thereby further boosting the carry trade by speculation of further exchange rate rises.
Thus the currencies of deficit countries appreciated, making their goods less competitive and worsening their current account deficit. Between 1996 and 2006, the average current account deficits as a percentage of GDP for Australia, the USA and the UK were close to 4½, 4 and 2, respectively. Between January 1996 and December 2006, the broad-based real exchange rate index of the Australian dollar appreciated by 17%, of the US dollar by 4% and of sterling by some 23%.
 Currencies of surplus countries depreciated, making their goods more competitive and further boosting their current account surpluses. For example, between 2004 and 2006 the average current account surpluses as a percentage of GDP for Japan and Switzerland were 3½ and 13, respectively. Their short-term interest rates averaged a mere 0.1% and 1.0% respectively (compared with 3.4%, 4.7% and 5.7% for the USA, the UK and Australia). Yet between January 2004 and December 2006, the real exchange rate index of the yen depreciated by 21%, while that of the Swiss franc depreciated by 6%.
Currencies of surplus countries depreciated, making their goods more competitive and further boosting their current account surpluses. For example, between 2004 and 2006 the average current account surpluses as a percentage of GDP for Japan and Switzerland were 3½ and 13, respectively. Their short-term interest rates averaged a mere 0.1% and 1.0% respectively (compared with 3.4%, 4.7% and 5.7% for the USA, the UK and Australia). Yet between January 2004 and December 2006, the real exchange rate index of the yen depreciated by 21%, while that of the Swiss franc depreciated by 6%.
With the credit crunch of 2007/8, the carry trade unwound. Much of the money deposited in the USA had been in highly risky assets, such as sub-prime mortgages. Investors scrambled to sell their assets in the USA, UK and the EU. Loans from Japan and Switzerland were repaid and these countries, seen as ‘safe havens’, attracted deposits. The currencies of deficit countries, such as the UK and USA, began to depreciate and those of surplus countries, such as Japan and Switzerland, began to appreciate. Between September 2007 and September 2008, the real exchange rate indices of the US dollar and sterling depreciated by 2% and 13% respectively; the yen and the Swiss franc appreciated by 3% and 2¾%.
This represented a ‘double whammy’ for Japanese exporters. Not only did its currency appreciate, making its exports more expensive in dollars, euros, pounds, etc., but the global recession saw consumers around the world buying less. As a result, the Japanese economy suffered the worst recession of the G7 economies.
The carry trade in recent months
Since 2016, there has been a re-emergence of the carry trade as the Fed began raising interest rates while the Bank of Japan kept rates at the ultra low level of –0.1% (see Figure 1). The process slowed down when the USA lowered interest rates in 2020 in response to the pandemic and fears of recession. But when the USA, the EU and the UK began raising rates at the beginning of 2022 in response to global inflationary pressures, while Japan kept its main rate at –0.1%, so the carry trade resumed in earnest. Cross-border loans originating in Japan (not all of it from the carry trade) had risen to ¥157tn ($1tn) by March 2024 – a rise of 21% from 2021.
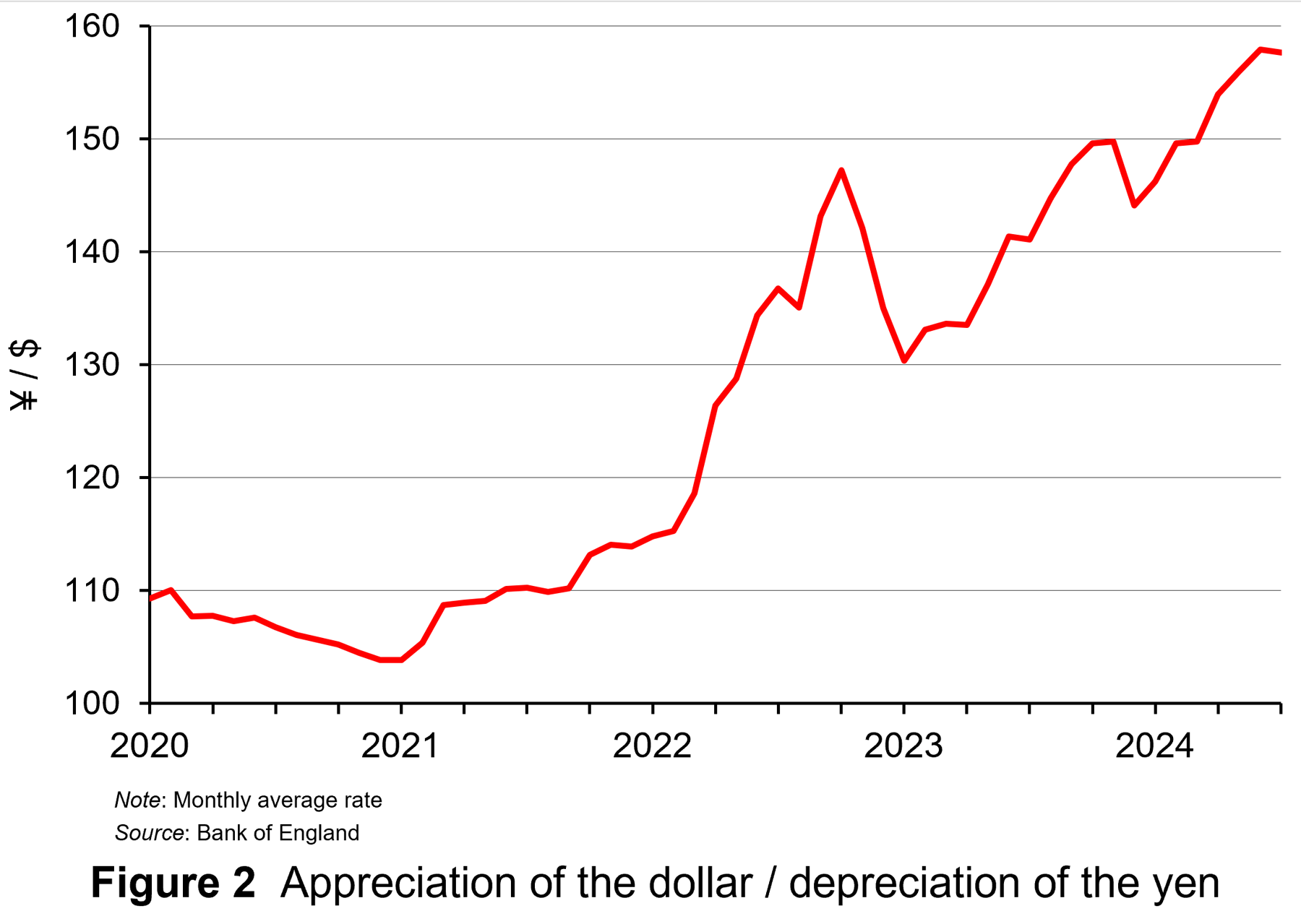 The process boosted US stock markets and contributed to the dollar appreciating against the yen (see Figure 2: click here for a PowerPoint).
The process boosted US stock markets and contributed to the dollar appreciating against the yen (see Figure 2: click here for a PowerPoint).
Although this depreciation of the yen helped Japanese exports, it also led to rising prices. Japanese inflation rose steadily throughout 2022. In the 12 months to January 2022 the inflation rate was 0.5% (having been negative from October 2020 to August 2021). By January 2023, the annual rate had risen to 4.3% – a rate not seen since 1981. The Bank of Japan was cautious about raising interest rates to suppress this inflation, however, for fear of damaging growth and causing the exchange rate to appreciate and thereby damaging exports. Indeed, quarterly economic growth fell from 1.3% in 2023 Q1 to –1.0% in 2023 Q3.
But then, with growth rebounding and the yen depreciating further, in March 2024 the Bank of Japan decided to raise its key rate from –0.1% to 0.1%. This initially had the effect of stabilising the exchange rate. But then with the yen depreciating further and inflation rising from 2.5% to 2.8% in May and staying at this level in June, the Bank of Japan increased the key rate again at the end of July – this time to 0.25% – and there were expectations that there would be another rise before the end of the year.
At the same time, there were expectations that the Fed would soon lower its main rate (the Federal Funds Rate) from its level of 5.33%. The ECB and the Bank of England had already begun lowering their main rates in response to lower inflation. The carry trade rapidly unwound. Investors sold US, EU and UK assets and began repaying yen loans.
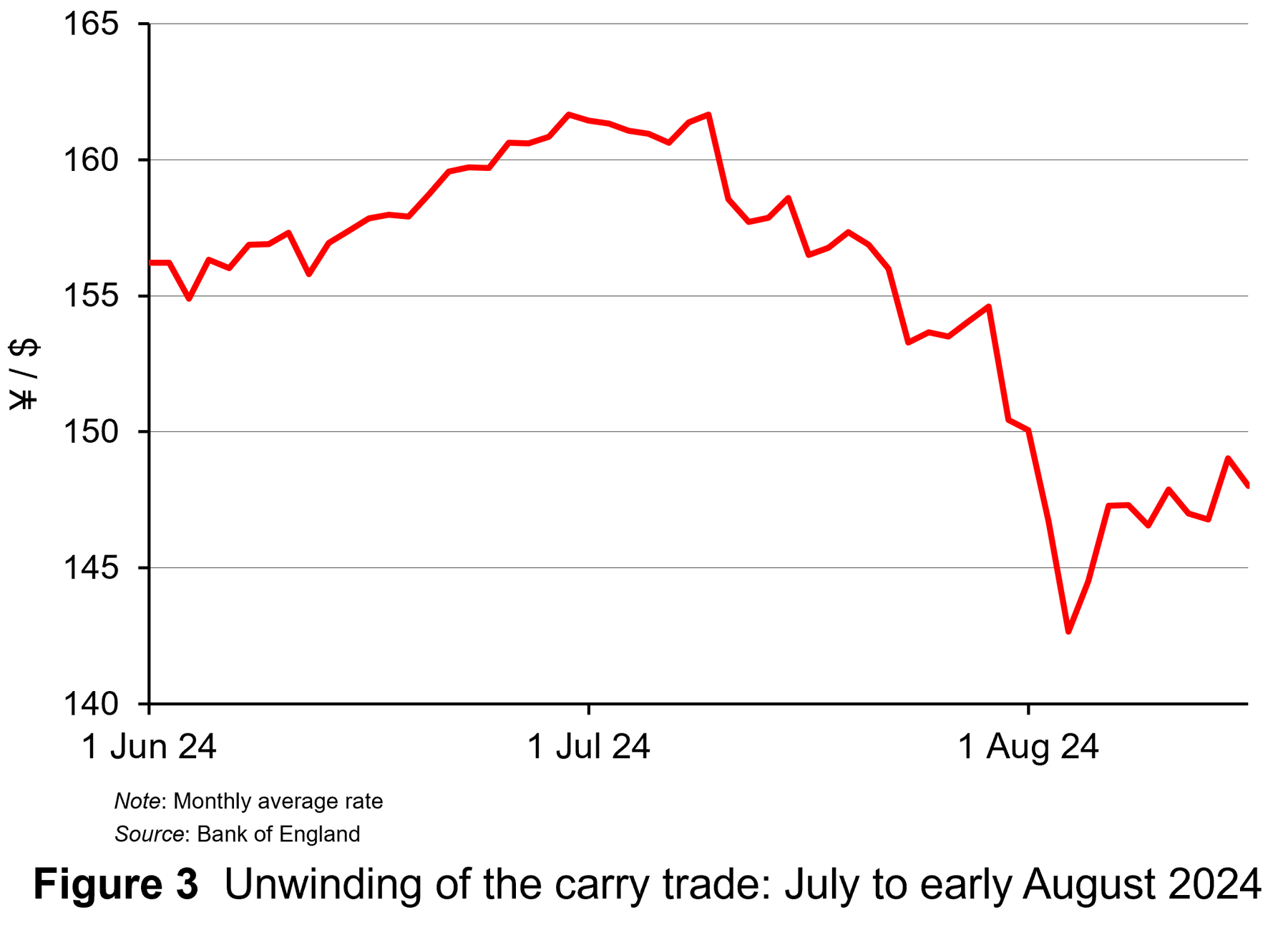 The result was a rapid appreciation of the yen as Figure 3 shows (click here for a PowerPoint). Between 31 July (the date the Bank of Japan raised interest rates the second time) and 5 August, the dollar depreciated against the yen from ¥150.4 to ¥142.7. In other words, the value of 100 yen appreciated from $0.66 to $0.70 – an appreciation of the yen of 6.1%.
The result was a rapid appreciation of the yen as Figure 3 shows (click here for a PowerPoint). Between 31 July (the date the Bank of Japan raised interest rates the second time) and 5 August, the dollar depreciated against the yen from ¥150.4 to ¥142.7. In other words, the value of 100 yen appreciated from $0.66 to $0.70 – an appreciation of the yen of 6.1%.
Fears about the unwinding of the carry trade led to falls in stock markets around the world. Not only were investors selling shares to pay back the loans, but fears of the continuing process put further downward pressure on shares. From 31 July to 5 August, the US S&P 500 fell by 6.1% and the tech-heavy Nasdaq by 8.0%.
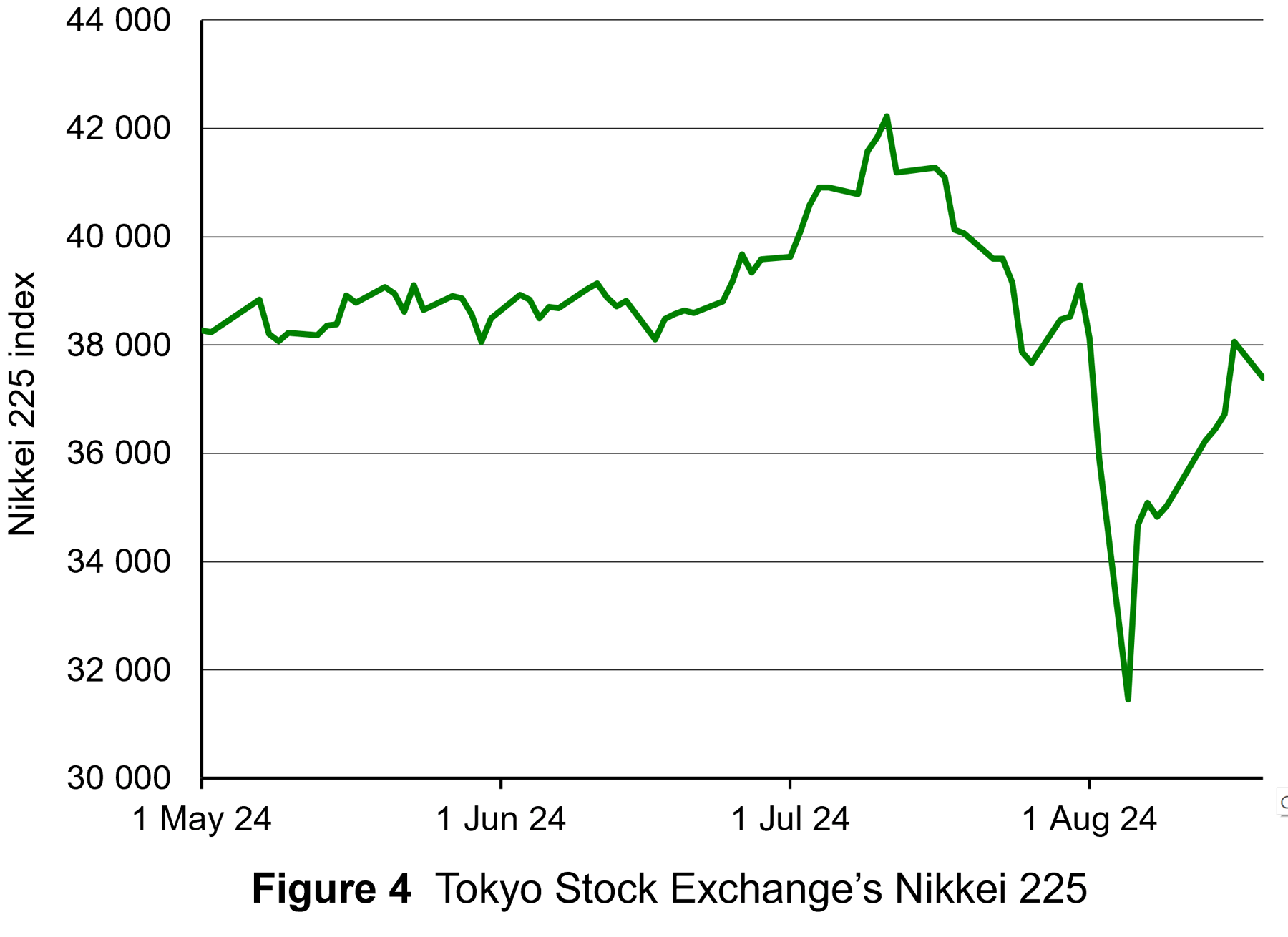 As far as the Tokyo stock market was concerned, the appreciation of the yen sparked fears that the large Japanese export sector would be damaged. Investors rushed to sell shares. Between 31 July and 5 August, the Nikkei 225 (the main Japanese stock market index) fell by 19.5% – its biggest short-term fall ever (see Figure 4: click here for a PowerPoint).
As far as the Tokyo stock market was concerned, the appreciation of the yen sparked fears that the large Japanese export sector would be damaged. Investors rushed to sell shares. Between 31 July and 5 August, the Nikkei 225 (the main Japanese stock market index) fell by 19.5% – its biggest short-term fall ever (see Figure 4: click here for a PowerPoint).
Although the yen has since depreciated slightly (a rise in the yen/dollar rate) and stock markets have recovered somewhat, expectations of many investors are that the unwinding of the yen carry trade has some way to go. This could result in a further appreciation of the yen from current levels of around ¥100 = $0.67 to around $0.86 in a couple of years’ time.
There are also fears about the carry trade in the Chinese currency, the yuan. Some $500 billion of foreign currency holdings have been acquired with yuan since 2022. As with the Japanese carry trade, this has been encouraged by low Chinese interest rates and a depreciating yuan. Not only are Chinese companies investing abroad, but foreign companies operating in China have been using their yuan earnings from their Chinese operations to invest abroad rather than in China. The Chinese carry trade, however, has been restricted by the limited convertibility of the yuan. If the Chinese carry trade begins to unwind when the Chinese economy begins to recover and interest rates begin to rise, the effect will probably be more limited than with the yen.
Articles
- A popular trading strategy just blew up in investors’ faces
CNN, Allison Morrow (7/8/24)
- The big ‘carry trade’ unwind is far from over, strategists warn
CNBC, Sam Meredith (13/8/24)
- Unwinding of yen ‘carry trade’ still threatens markets, say analysts
Financial Times, Leo Lewis and David Keohane (7/8/24)
- The yen carry trade sell-off marks a step change in the business cycle
Financial Times, John Plender (10/8/24)
- Forbes Money Markets Global Markets React To The Japanese Yen Carry Trade Unwind
Forbes, Frank Holmes (12/8/24)
- 7 unwinding carry trades that crashed the markets
Alt21 (26/1/23)
- A carry crash also kicked off the global financial crisis 17 years ago — here’s why it’s unlikely to get as bad this time
The Conversation, Charles Read (9/8/24)
- What is the Chinese yuan carry trade and how is it different from the yen’s?
Reuters, Winni Zhou and Summer Zhen (13/8/24)
- Carry Trade That Blew Up Markets Is Attracting Hedge Funds Again
Yahoo Finance/Bloomberg, David Finnerty and Ruth Carson (16/8/24)
- Currency Carry Trades 101
Investopedia, Kathy Lien (9/8/24)
- Carry Trades Torpedoed The Market. They’re Still Everywhere.
Finimize, Stéphane Renevier (13/8/24)
Questions
- What factors drive the currency carry trade?
- Is the carry trade a form of arbitrage?
- Find out and explain what has happened to the Japanese yen since this blog was written.
- Find out and explain some other examples of carry trades.
- Why are expectations so important in determining the extent and timing of the unwinding of carry trades?
 The past decade or so has seen large-scale economic turbulence. As we saw in the blog Fiscal impulses, governments have responded with large fiscal interventions. The COVID-19 pandemic, for example, led to a positive fiscal impulse in the UK in 2020, as measured by the change in the structural primary balance, of over 12 per cent of national income.
The past decade or so has seen large-scale economic turbulence. As we saw in the blog Fiscal impulses, governments have responded with large fiscal interventions. The COVID-19 pandemic, for example, led to a positive fiscal impulse in the UK in 2020, as measured by the change in the structural primary balance, of over 12 per cent of national income.
The scale of these interventions has led to a significant increase in the public-sector debt-to-GDP ratio in many countries. The recent interest rates hikes arising from central banks responding to inflationary pressures have put additional pressure on the financial well-being of governments, not least on the financing of their debt. Here we discuss these pressures in the context of the ‘r – g’ rule of sustainable public debt.
Public-sector debt and borrowing
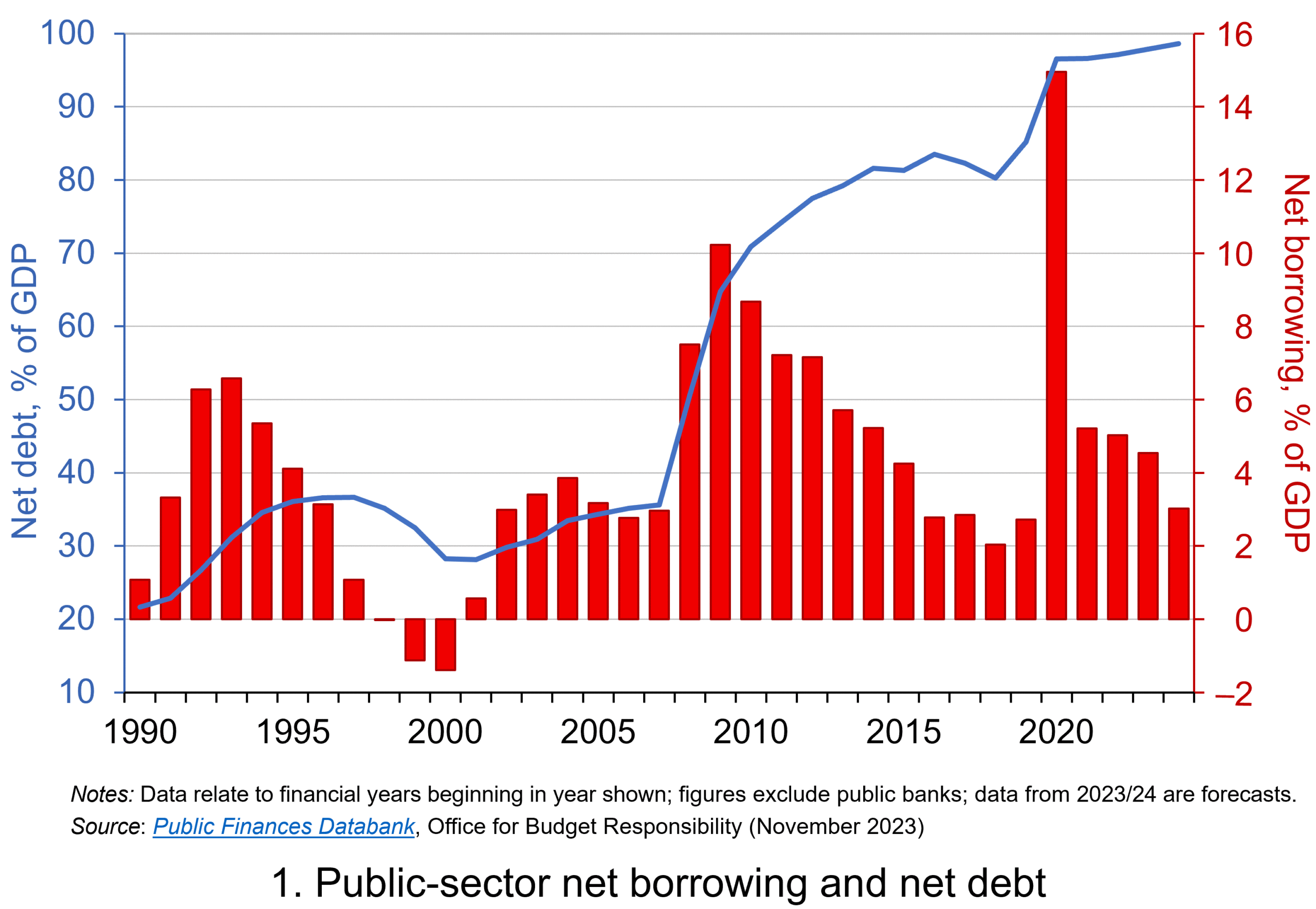 Chart 1 shows the path of UK public-sector net debt and net borrowing, as percentages of GDP, since 1990. Debt is a stock concept and is the result of accumulated flows of past borrowing. Net debt is simply gross debt less liquid financial assets, which mainly consist of foreign exchange reserves and cash deposits. Net borrowing is the headline measure of the sector’s deficit and is based on when expenditures and receipts (largely taxation) are recorded rather than when cash is actually paid or received. (Click here for a PowerPoint of Chart 1)
Chart 1 shows the path of UK public-sector net debt and net borrowing, as percentages of GDP, since 1990. Debt is a stock concept and is the result of accumulated flows of past borrowing. Net debt is simply gross debt less liquid financial assets, which mainly consist of foreign exchange reserves and cash deposits. Net borrowing is the headline measure of the sector’s deficit and is based on when expenditures and receipts (largely taxation) are recorded rather than when cash is actually paid or received. (Click here for a PowerPoint of Chart 1)
Chart 1 shows the impact of the fiscal interventions associated with the global financial crisis and the COVID-19 pandemic, when net borrowing rose to 10 per cent and 15 per cent of GDP respectively. The former contributed to the debt-to-GDP ratio rising from 35.6 per cent in 2007/8 to 81.6 per cent in 2014/15, while the pandemic and subsequent cost-of-living interventions contributed to the ratio rising from 85.2 per cent in 2019/20 to around 98 per cent in 2023/24.
Sustainability of the public finances
 The ratcheting up of debt levels affects debt servicing costs and hence the budgetary position of government. Yet the recent increases in interest rates also raise the costs faced by governments in financing future deficits or refinancing existing debts that are due to mature. In addition, a continuation of the low economic growth that has beset the UK economy since the global financial crisis also has implications for the burden imposed on the public sector by its debts, and hence the sustainability of the public finances. After all, low growth has implications for spending commitments, and, of course, the flow of receipts.
The ratcheting up of debt levels affects debt servicing costs and hence the budgetary position of government. Yet the recent increases in interest rates also raise the costs faced by governments in financing future deficits or refinancing existing debts that are due to mature. In addition, a continuation of the low economic growth that has beset the UK economy since the global financial crisis also has implications for the burden imposed on the public sector by its debts, and hence the sustainability of the public finances. After all, low growth has implications for spending commitments, and, of course, the flow of receipts.
The analysis therefore implies that the sustainability of public-sector debt is dependent on at least three factors: existing debt levels, the implied average interest rate facing the public sector on its debts, and the rate of economic growth. These three factors turn out to underpin a well-known rule relating to the fiscal arithmetic of public-sector debt. The rule is sometimes known as the ‘r – g’ rule (i.e. the interest rate minus the growth rate).
Underpinning the fiscal arithmetic that determines the path of public-sector debt is the concept of the ‘primary balance’. This is the difference between the sector’s receipts and its expenditures less its debt interest payments. A primary surplus (a positive primary balance) means that receipts exceed expenditures less debt interest payments, whereas a primary deficit (a negative primary balance) means that receipts fall short. The fiscal arithmetic necessary to prevent the debt-to-GDP ratio rising produces the following stable debt equation or ‘r – g’ rule:
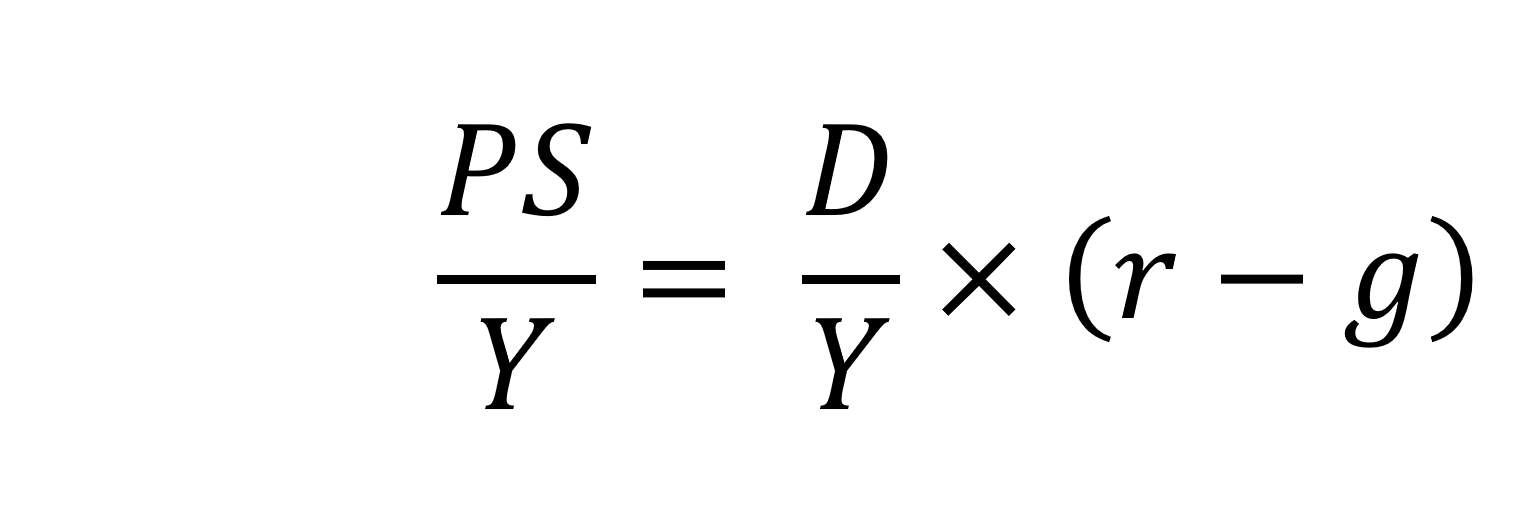
On the left-hand side of the stable debt equation is the required primary surplus (PS) to GDP (Y) ratio. Moving to the right-hand side, the first term is the existing debt-to-GDP ratio (D/Y). The second term ‘r – g’, is the differential between the average implied interest rate the government pays on its debt and the growth rate of the economy. These terms can be expressed in either nominal or real terms as this does not affect the differential.
To illustrate the rule consider a country whose existing debt-to-GDP ratio is 1 (i.e. 100 per cent) and the ‘r – g’ differential is 0.02 (2 percentage points). In this scenario they would need to run a primary surplus to GDP ratio of 0.02 (i.e. 2 percent of GDP).
The ‘r – g‘ differential
The ‘r – g’ differential reflects macroeconomic and financial conditions. The fiscal arithmetic shows that these are important for the dynamics of public-sector debt. The fiscal arithmetic is straightforward when r = g as any primary deficit will cause the debt-to-GDP ratio to rise, while a primary surplus will cause the ratio to fall. The larger is g relative to r the more favourable are the conditions for the path of debt. Importantly, if the differential is negative (r < g), it is possible for the public sector to run a primary deficit, up to the amount that the stable debt equation permits.
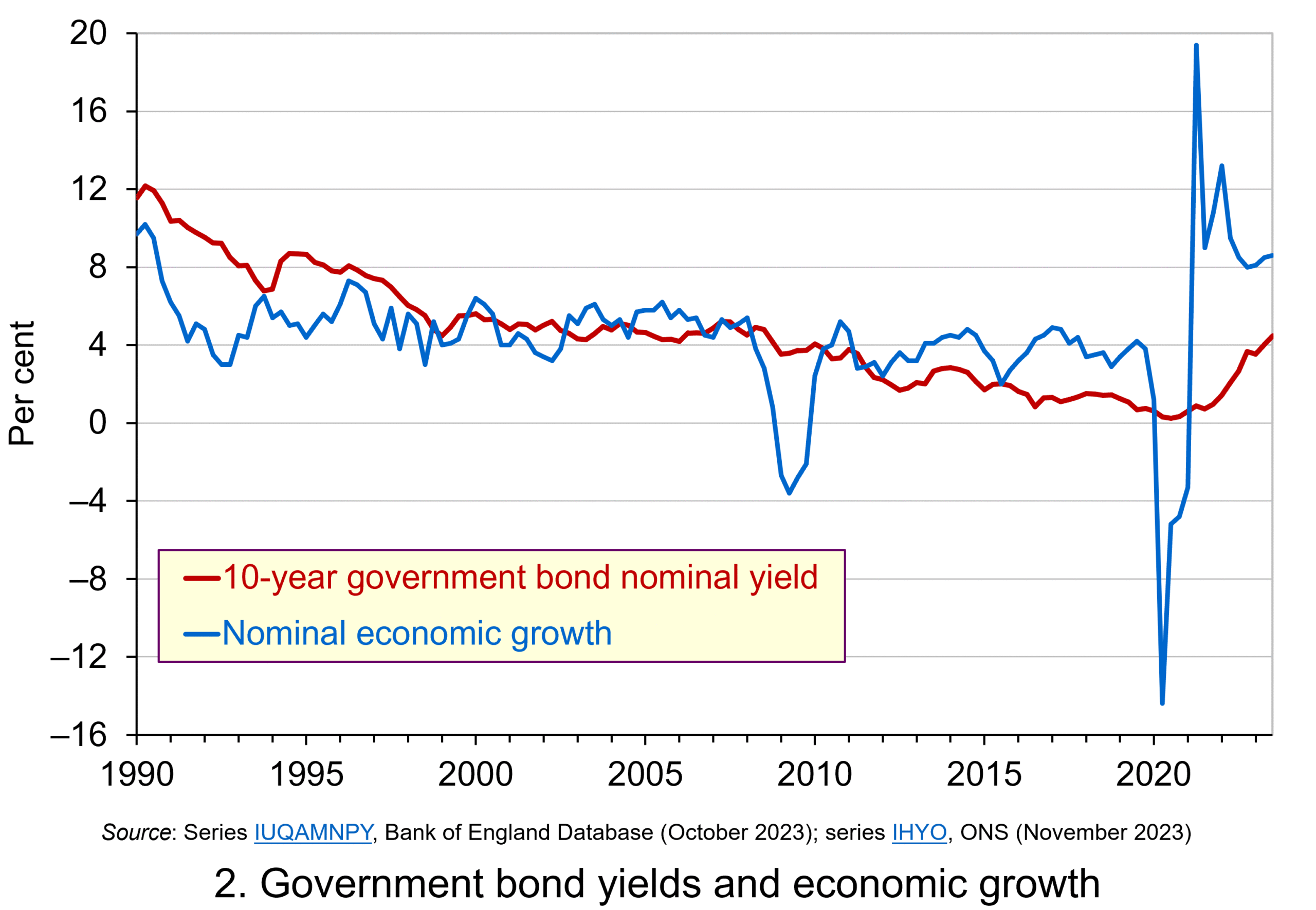 Consider Charts 2 and 3 to understand how the ‘r – g’ differential has affected debt sustainability in the UK since 1990. Chart 2 plots the implied yield on 10-year government bonds, alongside the annual rate of nominal growth (click here for a PowerPoint). As John explains in his blog The bond roller coaster, the yield is calculated as the coupon rate that would have to be paid for the market price of a bond to equal its face value. Over the period, the average annual nominal growth rate was 4.5 per cent, while the implied interest rate was almost identical at 4.6 per cent. The average annual rate of CPI inflation over this period was 2.8 per cent.
Consider Charts 2 and 3 to understand how the ‘r – g’ differential has affected debt sustainability in the UK since 1990. Chart 2 plots the implied yield on 10-year government bonds, alongside the annual rate of nominal growth (click here for a PowerPoint). As John explains in his blog The bond roller coaster, the yield is calculated as the coupon rate that would have to be paid for the market price of a bond to equal its face value. Over the period, the average annual nominal growth rate was 4.5 per cent, while the implied interest rate was almost identical at 4.6 per cent. The average annual rate of CPI inflation over this period was 2.8 per cent.
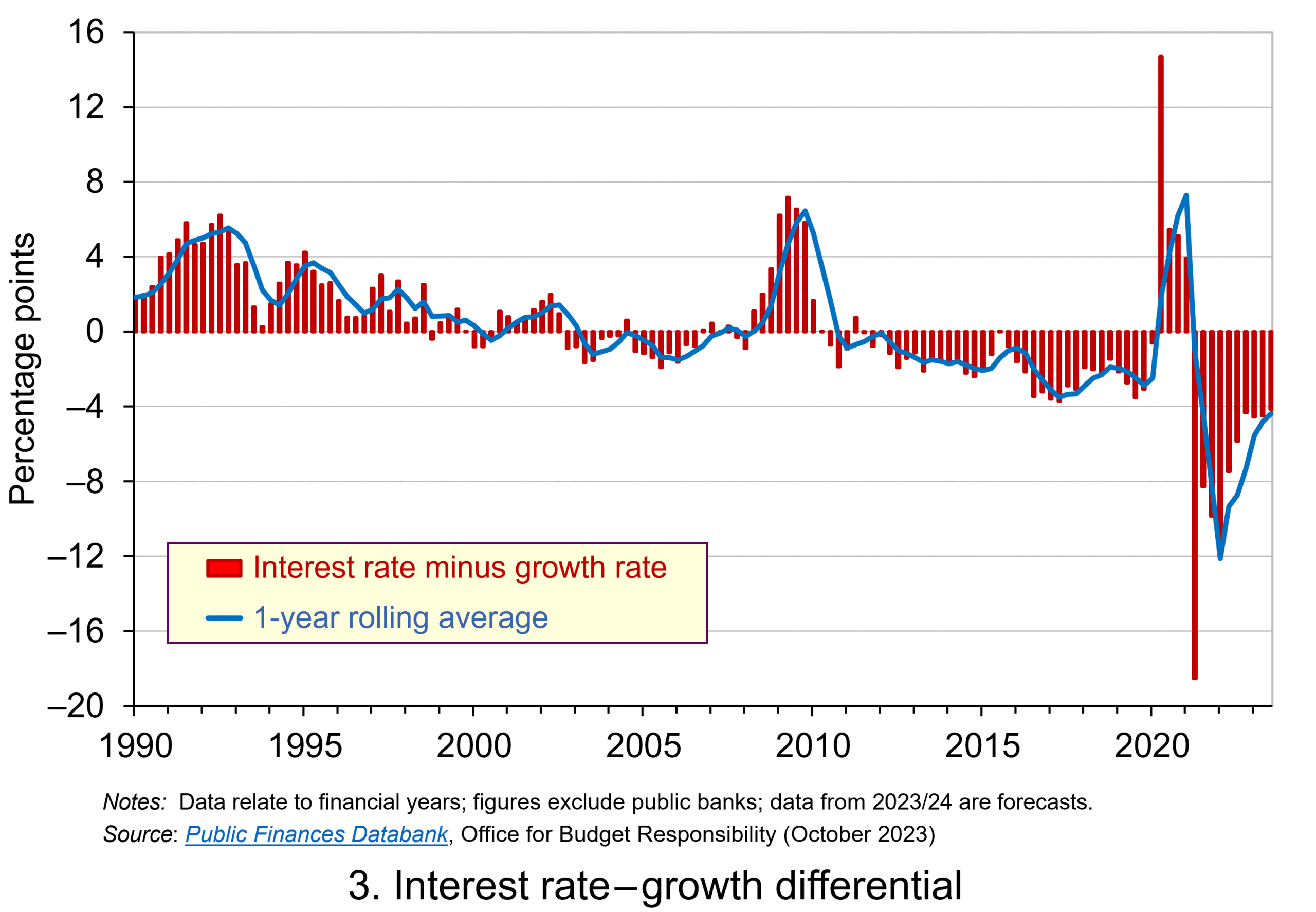 Chart 3 plots the ‘r – g’ differential which is simply the difference between the two series in Chart 2, along with a 12-month rolling average of the differential to help show better the direction of the differential by smoothing out some of the short-term volatility (click here for a PowerPoint). The differential across the period is a mere 0.1 percentage points implying that macroeconomic and financial conditions have typically been neutral in supporting debt sustainability. However, this does mask some significant changes across the period.
Chart 3 plots the ‘r – g’ differential which is simply the difference between the two series in Chart 2, along with a 12-month rolling average of the differential to help show better the direction of the differential by smoothing out some of the short-term volatility (click here for a PowerPoint). The differential across the period is a mere 0.1 percentage points implying that macroeconomic and financial conditions have typically been neutral in supporting debt sustainability. However, this does mask some significant changes across the period.
We observe a general downward trend in the ‘r – g’ differential from 1990 up to the time of the global financial crisis. Indeed between 2003 and 2007 we observe a favourable negative differential which helps to support the sustainability of public debt and therefore the well-being of the public finances. This downward trend of the ‘r – g’ differential was interrupted by the financial crisis, driven by a significant contraction in economic activity. This led to a positive spike in the differential of over 7 percentage points.
 Yet the negative differential resumed in 2010 and continued up to the pandemic. Again, this is indicative of the macroeconomic and financial environments being supportive of the public finances. It was, however, largely driven by low interest rates rather than by economic growth.
Yet the negative differential resumed in 2010 and continued up to the pandemic. Again, this is indicative of the macroeconomic and financial environments being supportive of the public finances. It was, however, largely driven by low interest rates rather than by economic growth.
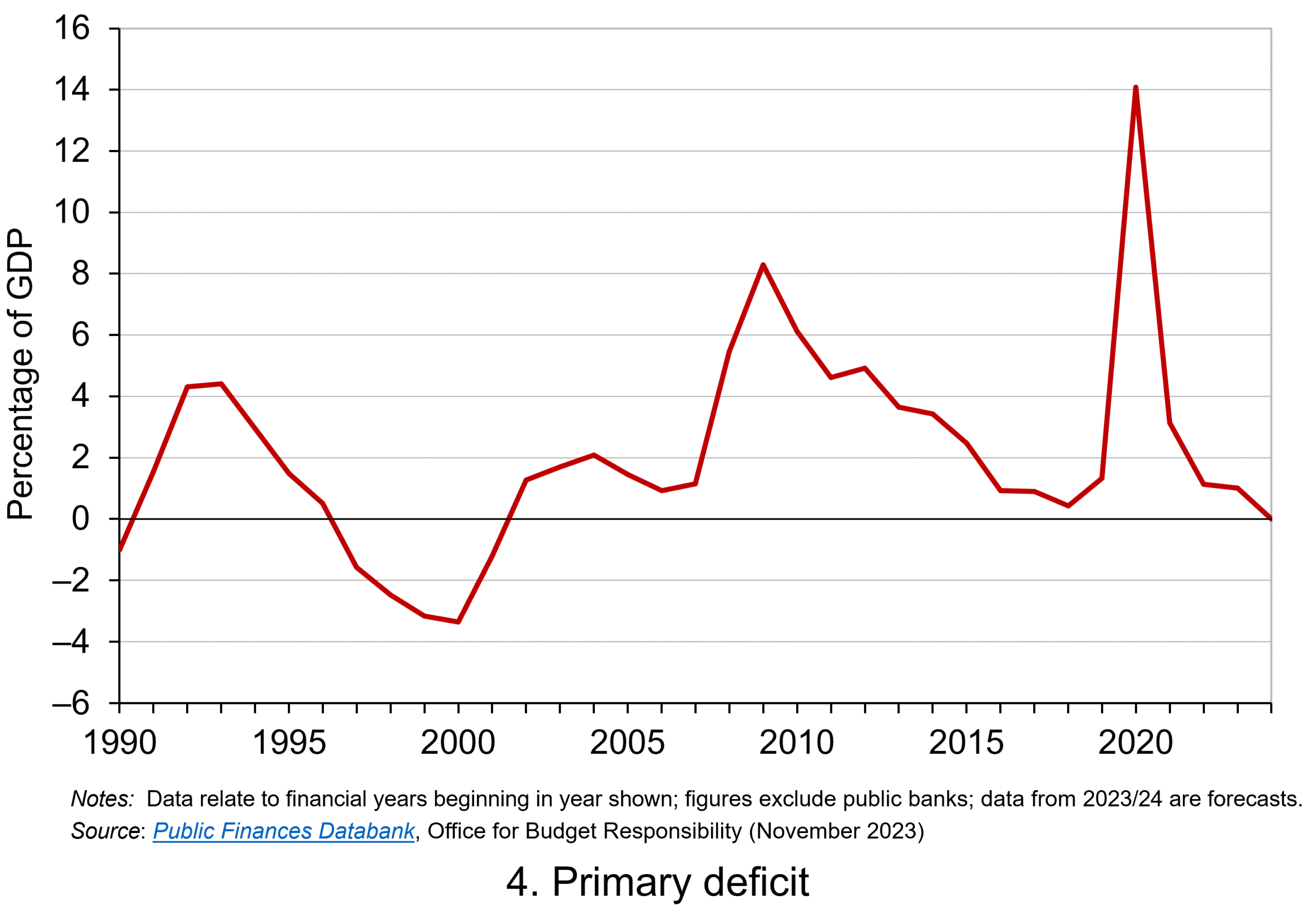
Consequently, the negative ‘r – g’ differential meant that the public sector could continue to run primary deficits during the 2010s, despite the now much higher debt-to-GDP ratio. Yet, weak growth was placing limits on this. Chart 4 indeed shows that primary deficits fell across the decade (click here for a PowerPoint).
The pandemic and beyond
 The pandemic saw the ‘r – g’ differential again turn markedly positive, averaging 7 percentage points in the four quarters from Q2 of 2020. While the differential again turned negative, the debt-to-GDP ratio had also increased substantially because of large-scale fiscal interventions. This made the negative differential even more important for the sustainability of the public finances. The question is how long the negative differential can last.
The pandemic saw the ‘r – g’ differential again turn markedly positive, averaging 7 percentage points in the four quarters from Q2 of 2020. While the differential again turned negative, the debt-to-GDP ratio had also increased substantially because of large-scale fiscal interventions. This made the negative differential even more important for the sustainability of the public finances. The question is how long the negative differential can last.
Looking forward, the fiscal arithmetic is indeed uncertain and worryingly is likely to be less favourable. Interest rates have risen and, although inflationary pressures may be easing somewhat, interest rates are likely to remain much higher than during the past decade. Geopolitical tensions and global fragmentation pose future inflationary concerns and a further drag on growth.
As well as the short-term concerns over growth, there remain long-standing issues of low productivity which must be tackled if the growth of the UK economy’s potential output is to be raised. These concerns all point to the important ‘r – g’ differential become increasingly less negative, if not positive. If so the fiscal arithmetic could mean increasingly hard maths for policymakers.
Articles
- The budget deficit: a short guide
House of Commons Library (8/6/23)
- If markets are right about long real rates, public debt ratios will increase for some time. We must make sure that they do not explode.
Peterson Institute for International Economics, Olivier Blanchard (6/11/23)
- The UK government’s debt nightmare
ITV News, Robert Peston (13/7/23)
- National debt could hit 300% of GDP by 2070s, independent watchdog the OBR warns
Sky News, James Sillars (13/7/23)
- How much money is the UK government borrowing, and does it matter?
BBC News (20/10/23)
- Cost of national debt hits 20-year high
BBC News, Vishala Sri-Pathma & Faisal Islam (4/10/23)
- Bond markets could see ‘mini boom-bust cycles’ as global government debt to soar by $5 trillion a yea
Markets Insider, Filip De Mott (16/11/23)
- The counterintuitive truth about deficits for bond investors
Financial Times, Matt King (17/11/23)
- UK government borrowing almost £20bn lower than expected
The Guardian, Richard Partington (20/10/23)
- Controlling debt is just a means — it is not a government’s end
Financial Times, Martin Wolf (13/11/23)
Data
Questions
- What is meant by each of the following terms: (a) net borrowing; (b) primary deficit; (c) net debt?
- Explain how the following affect the path of the public-sector debt-to-GDP ratio: (a) interest rates; (b) economic growth; (c) the existing debt-to-GDP ratio.
- Which factors during the 2010s were affecting the fiscal arithmetic of public debt positively, and which negatively?
- Discuss the prospects for the fiscal arithmetic of public debt in the coming years.
- Assume that a country has an existing public-sector debt-to-GDP ratio of 60 percent.
(a) Using the ‘rule of thumb’ for public debt dynamics, calculate the approximate primary balance it would need to run in the coming year if the expected average real interest rate on the debt were 3 per cent and real economic growth were 2 per cent?
(b) Repeat (a) but now assume that real economic growth is expected to be 4 per cent.
(c) Repeat (a) but now assume that the existing public-sector debt-to-GDP ratio is 120 per cent.
(d) Using your results from (a) to (c) discuss the factors that affect the fiscal arithmetic of the growth of public-sector debt.
 In his blog, The bond roller coaster, John looks at the pricing of government bonds and details how, in recent times, governments wishing to borrow by issuing new bonds are having to offer higher coupon rates to attract investors. The interest rate hikes by central banks in response to global-wide inflationary pressures have therefore spilt over into bond markets. Though this evidences the ‘pass through’ of central bank interest rate increases to the general structure of interest rates, it does, however, pose significant costs for governments as they seek to finance future budgetary deficits or refinance existing debts coming up to maturity.
In his blog, The bond roller coaster, John looks at the pricing of government bonds and details how, in recent times, governments wishing to borrow by issuing new bonds are having to offer higher coupon rates to attract investors. The interest rate hikes by central banks in response to global-wide inflationary pressures have therefore spilt over into bond markets. Though this evidences the ‘pass through’ of central bank interest rate increases to the general structure of interest rates, it does, however, pose significant costs for governments as they seek to finance future budgetary deficits or refinance existing debts coming up to maturity.
The Autumn Statement in the UK is scheduled to be made on 22 November. This, as well as providing an update on the economy and the public finances, is likely to include a number of fiscal proposals. It is thus timely to remind ourselves of the size of recent discretionary fiscal measures and their potential impact on the sustainability of the public finances. In this first of two blogs, we consider the former: the magnitude of recent discretionary fiscal policy changes.
First, it is important to define what we mean by discretionary fiscal policy. It refers to deliberate changes in government spending or taxation. This needs to be distinguished from the concept of automatic stabilisers, which relate to those parts of government budgets that automatically result in an increase (decrease) of spending or a decrease (increase) in tax payments when the economy slows (quickens).
The suitability of discretionary fiscal policy measures depends on the objectives they trying to fulfil. Discretionary measures can be implemented, for example, to affect levels of public-service provision, the distribution of income, levels of aggregate demand or to affect longer-term growth of aggregate supply. As we shall see in this blog, some of the large recent interventions have been conducted primarily to support and stabilise economic activity in the face of heightened economic volatility.
 Discretionary fiscal measures in the UK are usually announced in annual Budget statements in the House of Commons. These are normally in March, but discretionary fiscal changes can be made in the Autumn Statement too. The Autumn Statement of October 2022, for example, took on significant importance as the new Chancellor of the Exchequer, Jeremy Hunt, tried to present a ‘safe pair hands’ following the fallout and market turbulence in response to the fiscal statement by the former Chancellor, Kwasi Kwarteng, on 23 September that year.
Discretionary fiscal measures in the UK are usually announced in annual Budget statements in the House of Commons. These are normally in March, but discretionary fiscal changes can be made in the Autumn Statement too. The Autumn Statement of October 2022, for example, took on significant importance as the new Chancellor of the Exchequer, Jeremy Hunt, tried to present a ‘safe pair hands’ following the fallout and market turbulence in response to the fiscal statement by the former Chancellor, Kwasi Kwarteng, on 23 September that year.
The fiscal impulse
The large-scale economic turbulence of recent years associated first with the global financial crisis of 2007–9 and then with the COVID-19 pandemic and the cost-of-living crisis, has seen governments respond with significant discretionary fiscal measures. During the COVID-19 pandemic, examples of fiscal interventions in the UK included the COVID-19 Business Interruption Loan Scheme (CBILS), grants for retail, hospitality and leisure businesses, the COVID-19 Job Retention Scheme (better known as the furlough scheme) and the Self-Employed Income Support Scheme.
 The size of discretionary fiscal interventions can be measured by the fiscal impulse. This captures the magnitude of change in discretionary fiscal policy and thus the size of the stimulus. The concept is not to be confused with fiscal multipliers, which measure the impact of fiscal changes on economic outcomes, such as real national income and employment.
The size of discretionary fiscal interventions can be measured by the fiscal impulse. This captures the magnitude of change in discretionary fiscal policy and thus the size of the stimulus. The concept is not to be confused with fiscal multipliers, which measure the impact of fiscal changes on economic outcomes, such as real national income and employment.
By measuring fiscal impulses, we can analyse the extent to which a country’s fiscal stance has tightened, loosened, or remained unchanged. In other words, we are attempting to capture discretionary fiscal policy changes that result in structural changes in the government budget and, therefore, in structural changes in spending and/or taxation.
To measure structural changes in the public-sector’s budgetary position, we calculate changes in structural budget balances.
A budget balance is simply the difference between receipts (largely taxation) and spending. A budget surplus occurs when receipts are greater than spending, while a deficit (sometimes referred to as net borrowing) occurs if spending is greater than receipts.
A structural budget balance cyclically-adjusts receipts and spending and hence adjusts for the position of the economy in the business cycle. In doing so, it has the effect of adjusting both receipts and spending for the effect of automatic stabilisers. Another way of thinking about this is to ask what the balance between receipts and spending would be if the economy were operating at its potential output. A deterioration in a structural budget balance infers a rise in the structural deficit or fall in the structural surplus. This indicates a loosening of the fiscal stance. An improvement in the structural budget balance, by contrast, indicates a tightening.
The size of UK fiscal impulses
A frequently-used measure of the fiscal impulse involves the change in the cyclically-adjusted public-sector primary deficit.
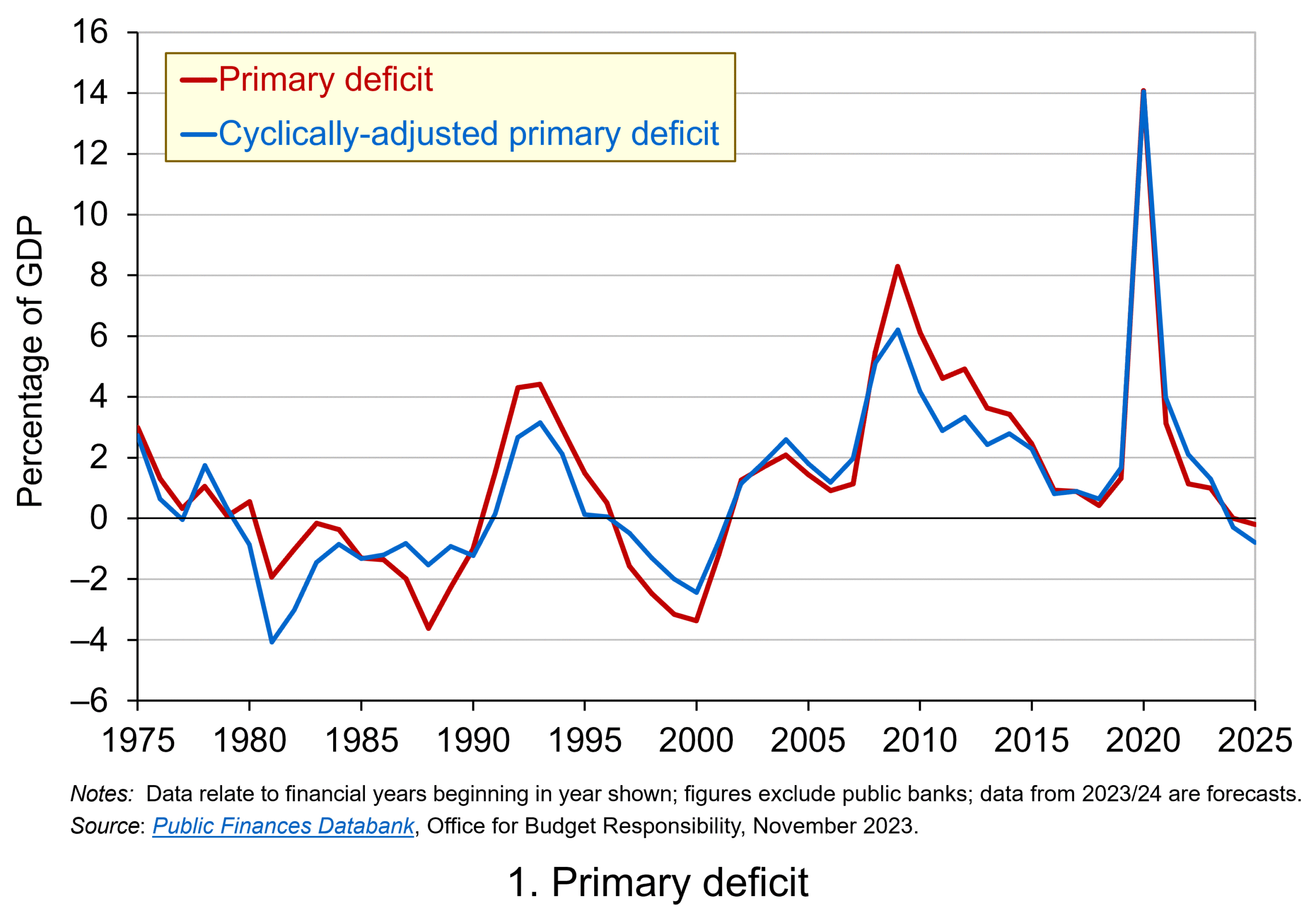 A primary deficit captures the extent to which the receipts of the public sector fall short of its spending, excluding its spending on debt interest payments. It essentially captures whether the public sector is able to afford its ‘new’ fiscal choices from its receipts; it excludes debt-servicing costs, which can be thought of as reflecting fiscal choices of the past. By using a cyclically-adjusted primary deficit we are able to isolate more accurately the size of discretionary policy changes. Chart 1 shows the UK’s actual and cyclically-adjusted primary deficit as a share of GDP since 1975, which have averaged 1.3 and 1.1 per cent of GDP respectively. (Click here for a PowerPoint of the chart.)
A primary deficit captures the extent to which the receipts of the public sector fall short of its spending, excluding its spending on debt interest payments. It essentially captures whether the public sector is able to afford its ‘new’ fiscal choices from its receipts; it excludes debt-servicing costs, which can be thought of as reflecting fiscal choices of the past. By using a cyclically-adjusted primary deficit we are able to isolate more accurately the size of discretionary policy changes. Chart 1 shows the UK’s actual and cyclically-adjusted primary deficit as a share of GDP since 1975, which have averaged 1.3 and 1.1 per cent of GDP respectively. (Click here for a PowerPoint of the chart.)
The size of the fiscal impulse is measured by the year-on-year percentage point change in the cyclically-adjusted public-sector primary deficit as a percentage of GDP. A larger deficit or a smaller surplus indicates a fiscal loosening (a positive fiscal impulse), while a smaller deficit or a larger surplus indicates a fiscal tightening (a negative fiscal impulse).
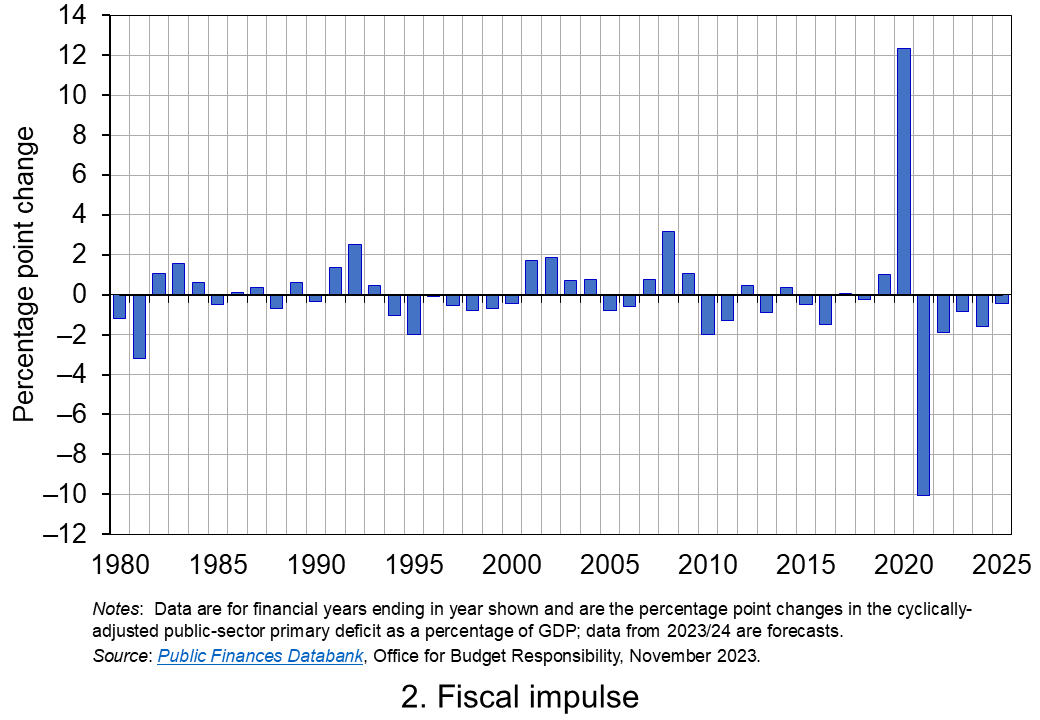 Chart 2 shows the magnitude of UK fiscal impulses since 1980. It captures very starkly the extent of the loosening of the fiscal stance in 2020 in response to the COVID-19 pandemic. (Click here for a PowerPoint of the chart.) In 2020 the cyclically-adjusted primary deficit to GDP ratio rose from 1.67 to 14.04 per cent. This represents a positive fiscal impulse of 12.4 per cent of GDP.
Chart 2 shows the magnitude of UK fiscal impulses since 1980. It captures very starkly the extent of the loosening of the fiscal stance in 2020 in response to the COVID-19 pandemic. (Click here for a PowerPoint of the chart.) In 2020 the cyclically-adjusted primary deficit to GDP ratio rose from 1.67 to 14.04 per cent. This represents a positive fiscal impulse of 12.4 per cent of GDP.
A tightening of fiscal policy followed the waning of the pandemic. 2021 saw a negative fiscal impulse of 10.1 per cent of GDP. Subsequent tightening was tempered by policy measures to limit the impact on the private sector of the cost-of-living crisis, including the Energy Price Guarantee and Energy Bills Support Scheme.
In comparison, the fiscal response to the global financial crisis led to a cumulative increase in the cyclically-adjusted primary deficit to GDP ratio from 2007 to 2009 of 5.0 percentage points. Hence, the financial crisis saw a positive fiscal impulse of 5 per cent of GDP. While smaller in comparison to the discretionary fiscal responses to the COVID-19 pandemic, it was, nonetheless, a sizeable loosening of the fiscal stance.
Sustainability and well-being of the public finances
The recent fiscal interventions have implications for the financial well-being of the public-sector. Not least, the financing of the positive fiscal impulses has led to a substantial growth in the accumulated size of the public-sector debt stock. At the end of 2006/7 the public-sector net debt stock was 35 per cent of GDP; at the end of the current financial year, 2023/24, it is expected to be 103 per cent.
As we saw at the outset, in an environment of rising interest rates, the increase in the public-sector debt to GDP ratio creates significant additional costs for government, a situation that is made more difficult for government not only by the current flatlining of economic activity, but by the low underlying rate of economic growth seen since the financial crisis. The combination of higher interest rates and lower economic growth has adverse implications for the sustainability of the public finances and the ability of the public sector to absorb the effects of future economic crises.
Articles
- Autumn Statement 2023: When is it and how will it affect me?
BBC News (16/11/23)
- What is the Autumn Statement?
House of Commons Library (13/11/23)
- Putting the fiscal toothpaste back into the tube: It’s time to normalise the euro area fiscal stance in 2024
VoxEU, Niels Thygesen, Roel Beetsma, Massimo Bordignon, Xavier Debrun, Mateusz Szczurek, Martin Larch, Matthias Busse, Mateja Gabrijelcic, Laszlo Jankovics and Janis Malzubris (30/6/23)
- Euro zone should tighten fiscal policy in 2024 to curb inflation, European Fiscal Board says
Reuters, Jan Strupczewski (28/6/23)
- Hutchins Center Fiscal Impact Measure: Federal, State and Local Fiscal Policy and the Economy
Brookings, Eli Asdourian, Louise Sheiner, and Lorae Stojanovic (27/10/23)
Report
- IFS Green Budget
Institute for Fiscal Studies, Carl Emmerson, Paul Johnson and Ben Zaranko (eds) (October 2023)
Data
Questions
- Explain what is meant by the following fiscal terms: (a) structural deficit; (b) automatic stabilisers; (c) discretionary fiscal policy; (d) primary deficit.
- What is the difference between current and capital public expenditures? Give some examples of each.
- Consider the following two examples of public expenditure: grants from government paid to the private sector for the installation of energy-efficient boilers, and welfare payments to unemployed people. How are these expenditures classified in the public finances and what fiscal objectives do you think they meet?
- Which of the following statements about the primary balance is FALSE?
(a) In the presence of debt interest payments a primary deficit will be smaller than a budget deficit.
(b) In the presence of debt interest payments a primary surplus will be smaller than a budget surplus.
(c) The primary balance differs from the budget balance by the size of debt interest payments.
(d) None of the above.
- Explain the difference between a fiscal impulse and a fiscal multiplier.
- Why is low economic growth likely to affect the sustainability of the public finances? What other factors could also matter?
 Over the decades, economies have become increasingly interdependent. This process of globalisation has involved a growth in international trade, the spread of technology, integrated financial markets and international migration.
Over the decades, economies have become increasingly interdependent. This process of globalisation has involved a growth in international trade, the spread of technology, integrated financial markets and international migration.
When the global economy is growing, globalisation spreads the benefits around the world. However, when there are economic problems in one part of the world, this can spread like a contagion to other parts. This was clearly illustrated by the credit crunch of 2007–8. A crisis that started in the sub-prime market in the USA soon snowballed into a worldwide recession. More recently, the impact of Covid-19 on international supply chains has highlighted the dangers of relying on a highly globalised system of production and distribution. And more recently still, the war in Ukraine has shown the dangers of food and fuel dependency, with rapid rises in prices of basic essentials having a disproportionate effect on low-income countries and people on low incomes in richer countries.
Moves towards autarky
So is the answer for countries to become more self-sufficient – to adopt a policy of greater autarky? Several countries have moved in this direction. The USA under President Trump pursued a much more protectionist agenda than his predecessors. The UK, although seeking new post-Brexit trade relationships, has seen a reduction in trade as new barriers with the EU have reduced UK exports and imports as a percentage of GDP.  According to the Office for Budget Responsibility’s November 2022 Economic and Fiscal Outlook, Brexit will result in the UK’s trade intensity being 15 per cent lower in the long run than if it had remained in the EU.
According to the Office for Budget Responsibility’s November 2022 Economic and Fiscal Outlook, Brexit will result in the UK’s trade intensity being 15 per cent lower in the long run than if it had remained in the EU.
Many European countries are seeking to achieve greater energy self-sufficiency, both as a means of reducing reliance on Russian oil and gas, but also in pursuit of a green agenda, where a greater proportion of energy is generated from renewables. More generally, countries and companies are considering how to reduce the risks of relying on complex international supply chains.
Limits to the gains from trade
The gains from international trade stem partly from the law of comparative advantage, which states that greater levels of production can be achieved by countries specialising in and exporting those goods that can be produced at a lower opportunity cost and importing those in which they have a comparative disadvantage. Trade can also lead to the transfer of technology and a downward pressure on costs and prices through greater competition.
 But trade can increase dependence on unreliable supply sources. For example, at present, some companies are seeking to reduce their reliance on Taiwanese parts, given worries about possible Chinese actions against Taiwan.
But trade can increase dependence on unreliable supply sources. For example, at present, some companies are seeking to reduce their reliance on Taiwanese parts, given worries about possible Chinese actions against Taiwan.
Also, governments have been increasingly willing to support domestic industries with various non-tariff barriers to imports, especially since the 2007–8 financial crisis. Such measures include subsidies, favouring domestic firms in awarding government contracts and using regulations to restrict imports. These protectionist measures are often justified in terms of achieving security of supply. The arguments apply particularly starkly in the case of food. In the light of large price increases in the wake of the Ukraine war, many countries are considering how to increase food self-sufficiency, despite it being more costly.
Also, trade in goods involves negative environmental externalities, as freight transport, whether by sea, air or land, involves emissions and can add to global warming. In 2021, shipping emitted over 830m tonnes of CO2, which represents some 3% of world total CO2 emissions. In 2019 (pre-pandemic), the figure was 800m tonnes. The closer geographically the trading partner, the lower these environmental costs are likely to be.
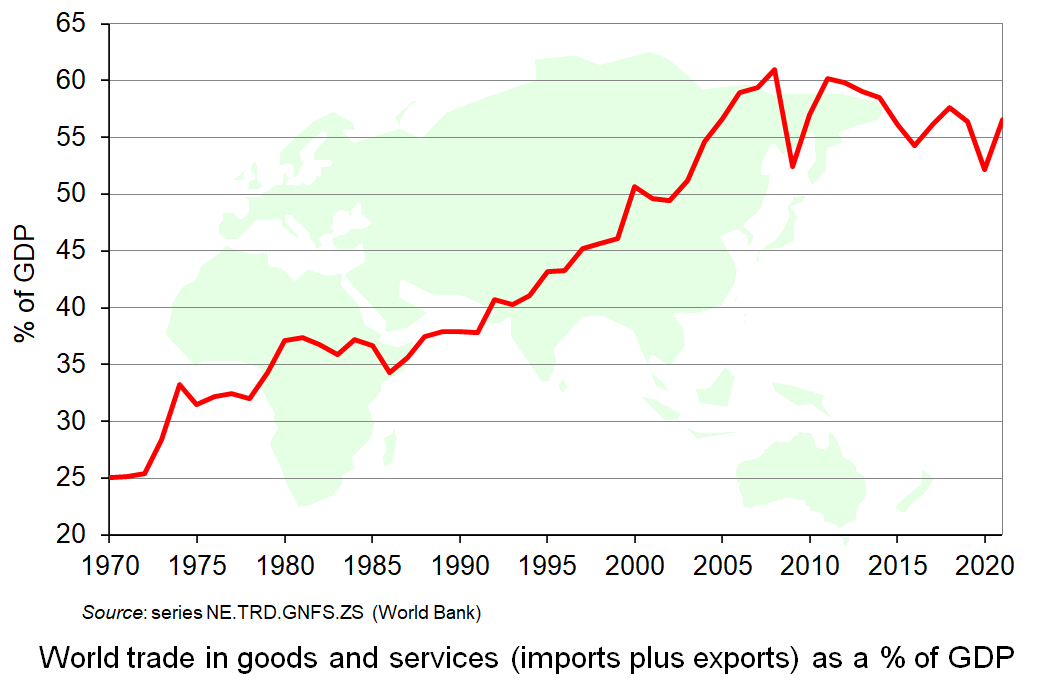 The problems with a globally interdependent world have led to world trade growing more slowly than world GDP in recent years after decades of trade growth considerably outstripping GDP growth. Trade (imports plus exports) as a percentage of GDP peaked at just over 60% in 2008. In 2019 and 2021 it was just over 56%. This is illustrated in the chart (click here for a PowerPoint). Although trade as a percentage of GDP rose slightly from 2020 to 2021 as economies recovered from the pandemic, it is expected to have fallen back again in 2022 and possibly further in 2023.
The problems with a globally interdependent world have led to world trade growing more slowly than world GDP in recent years after decades of trade growth considerably outstripping GDP growth. Trade (imports plus exports) as a percentage of GDP peaked at just over 60% in 2008. In 2019 and 2021 it was just over 56%. This is illustrated in the chart (click here for a PowerPoint). Although trade as a percentage of GDP rose slightly from 2020 to 2021 as economies recovered from the pandemic, it is expected to have fallen back again in 2022 and possibly further in 2023.
But despite this reduction in trade as a percentage of GDP, with de-globalisation likely to continue for some time, the world remains much more interdependent than in the more distant past (as the chart shows). Greater autarky may be seen as desirable by many countries as a response to the greater economic and political risks of the current world, but greater autarky is a long way from complete self-sufficiency. The world is likely to remain highly interdependent for the foreseeable future. Reports of the ‘death of globalisation’ are premature!
Podcasts
Articles
Report
Questions
- Explain the law of comparative advantage and demonstrate how trade between two countries can lead to both countries gaining.
- What are the main economic problems arising from globalisation?
- Is the answer to the problems of globalisation to move towards greater autarky?
- Would the expansion/further integration of trading blocs be a means of exploiting the benefits of globalisation while reducing the risks?
- Is the role of the US dollar likely to decline over time and, if so, why?
- Summarise Karl Polanyi’s arguments in The Great Transformation (see the Daniel W. Drezner article linked below). How well do they apply to the current world situation?
 We continue to live through incredibly turbulent times. In the past decade or so we have experienced a global financial crisis, a global health emergency, seen the UK’s departure from the European Union, and witnessed increasing levels of geopolitical tension and conflict. Add to this the effects from the climate emergency and it easy to see why the issue of economic uncertainty is so important when thinking about a country’s economic prospects.
We continue to live through incredibly turbulent times. In the past decade or so we have experienced a global financial crisis, a global health emergency, seen the UK’s departure from the European Union, and witnessed increasing levels of geopolitical tension and conflict. Add to this the effects from the climate emergency and it easy to see why the issue of economic uncertainty is so important when thinking about a country’s economic prospects. Figure 1 (click here for a PowerPoint) shows the WUI both globally and in the UK quarterly since 1991. The global index covers 143 countries and is presented as both a simple average and a GDP weighted average. The UK WUI is also shown. This is a three-quarter weighted average, the authors’ preferred measure for individual countries, where increasing weights of 0.1, 0.3 and 0.6 are used for the three most recent quarters.
Figure 1 (click here for a PowerPoint) shows the WUI both globally and in the UK quarterly since 1991. The global index covers 143 countries and is presented as both a simple average and a GDP weighted average. The UK WUI is also shown. This is a three-quarter weighted average, the authors’ preferred measure for individual countries, where increasing weights of 0.1, 0.3 and 0.6 are used for the three most recent quarters. As Figure 2 shows (click here for a PowerPoint), investment is particularly volatile, and much more so than household spending. Some of this can be attributed to the ‘lumpiness’ of investment decisions since these expenditures tend to be characterised by indivisibility and irreversibility. This means that they are often relatively costly to finance and are ‘all or nothing’ decisions. In the context of uncertainty, it can make sense therefore for firms to wait for news that makes the future clearer. In this sense, we can think of uncertainty rather like a fog that firms are peering through. The thicker the fog, the more uncertain the future and the more cautious firms are likely to be.
As Figure 2 shows (click here for a PowerPoint), investment is particularly volatile, and much more so than household spending. Some of this can be attributed to the ‘lumpiness’ of investment decisions since these expenditures tend to be characterised by indivisibility and irreversibility. This means that they are often relatively costly to finance and are ‘all or nothing’ decisions. In the context of uncertainty, it can make sense therefore for firms to wait for news that makes the future clearer. In this sense, we can think of uncertainty rather like a fog that firms are peering through. The thicker the fog, the more uncertain the future and the more cautious firms are likely to be.  The theory of buffer-stock saving was popularised by Christopher Carroll in 1992 (see link below). It implies that in the presence of uncertainty, people are prepared to consume less today in order to increase levels of saving, pay off existing debts, or borrow less relative to that in the absence of uncertainty. The extent of the buffer of financial wealth that people want to hold will depend on their own appetite for risk, the level of uncertainty, and the moderating effect from their own impatience and, hence, present bias for consuming today.
The theory of buffer-stock saving was popularised by Christopher Carroll in 1992 (see link below). It implies that in the presence of uncertainty, people are prepared to consume less today in order to increase levels of saving, pay off existing debts, or borrow less relative to that in the absence of uncertainty. The extent of the buffer of financial wealth that people want to hold will depend on their own appetite for risk, the level of uncertainty, and the moderating effect from their own impatience and, hence, present bias for consuming today. Figure 3 suggests that the relationship between confidence and uncertainty is rather more complex than perhaps is generally understood (click here for a PowerPoint). Haddow, Hare, Hooley and Shakir (see link below) argue that the evidence tends to point to changes in uncertainty affecting confidence, but with less evidence that changes in confidence affect uncertainty.
Figure 3 suggests that the relationship between confidence and uncertainty is rather more complex than perhaps is generally understood (click here for a PowerPoint). Haddow, Hare, Hooley and Shakir (see link below) argue that the evidence tends to point to changes in uncertainty affecting confidence, but with less evidence that changes in confidence affect uncertainty. A common practice of international investors is to take part in the so-called ‘carry trade’. This involves taking advantage of nominal interest rate differences between countries. For example, assume that interest rates are low in Japan and high in the USA. It is thus profitable to borrow yen in Japan at the low interest rate, exchange it into US dollars and deposit the money at the higher interest rate available in the USA. If there is no change in the exchange rate between the dollar and the yen, the investor makes a profit equal to the difference in the interest rates.
A common practice of international investors is to take part in the so-called ‘carry trade’. This involves taking advantage of nominal interest rate differences between countries. For example, assume that interest rates are low in Japan and high in the USA. It is thus profitable to borrow yen in Japan at the low interest rate, exchange it into US dollars and deposit the money at the higher interest rate available in the USA. If there is no change in the exchange rate between the dollar and the yen, the investor makes a profit equal to the difference in the interest rates. Prior to the financial crisis of 2008, current account deficit countries, such as the UK, USA and Australia, typically had relatively high interest rates, while current account surplus countries such as Japan and Switzerland had relatively low ones. Figure 1 shows central bank interest rates from 2005 to the current day (click
Prior to the financial crisis of 2008, current account deficit countries, such as the UK, USA and Australia, typically had relatively high interest rates, while current account surplus countries such as Japan and Switzerland had relatively low ones. Figure 1 shows central bank interest rates from 2005 to the current day (click  Currencies of surplus countries depreciated, making their goods more competitive and further boosting their current account surpluses. For example, between 2004 and 2006 the average current account surpluses as a percentage of GDP for Japan and Switzerland were 3½ and 13, respectively. Their short-term interest rates averaged a mere 0.1% and 1.0% respectively (compared with 3.4%, 4.7% and 5.7% for the USA, the UK and Australia). Yet between January 2004 and December 2006, the real exchange rate index of the yen depreciated by 21%, while that of the Swiss franc depreciated by 6%.
Currencies of surplus countries depreciated, making their goods more competitive and further boosting their current account surpluses. For example, between 2004 and 2006 the average current account surpluses as a percentage of GDP for Japan and Switzerland were 3½ and 13, respectively. Their short-term interest rates averaged a mere 0.1% and 1.0% respectively (compared with 3.4%, 4.7% and 5.7% for the USA, the UK and Australia). Yet between January 2004 and December 2006, the real exchange rate index of the yen depreciated by 21%, while that of the Swiss franc depreciated by 6%. The process boosted US stock markets and contributed to the dollar appreciating against the yen (see Figure 2: click
The process boosted US stock markets and contributed to the dollar appreciating against the yen (see Figure 2: click  The result was a rapid appreciation of the yen as Figure 3 shows (click
The result was a rapid appreciation of the yen as Figure 3 shows (click  As far as the Tokyo stock market was concerned, the appreciation of the yen sparked fears that the large Japanese export sector would be damaged. Investors rushed to sell shares. Between 31 July and 5 August, the Nikkei 225 (the main Japanese stock market index) fell by 19.5% – its biggest short-term fall ever (see Figure 4: click
As far as the Tokyo stock market was concerned, the appreciation of the yen sparked fears that the large Japanese export sector would be damaged. Investors rushed to sell shares. Between 31 July and 5 August, the Nikkei 225 (the main Japanese stock market index) fell by 19.5% – its biggest short-term fall ever (see Figure 4: click  The past decade or so has seen large-scale economic turbulence. As we saw in the blog
The past decade or so has seen large-scale economic turbulence. As we saw in the blog  Chart 1 shows the path of UK public-sector net debt and net borrowing, as percentages of GDP, since 1990. Debt is a stock concept and is the result of accumulated flows of past borrowing. Net debt is simply gross debt less liquid financial assets, which mainly consist of foreign exchange reserves and cash deposits. Net borrowing is the headline measure of the sector’s deficit and is based on when expenditures and receipts (largely taxation) are recorded rather than when cash is actually paid or received. (Click
Chart 1 shows the path of UK public-sector net debt and net borrowing, as percentages of GDP, since 1990. Debt is a stock concept and is the result of accumulated flows of past borrowing. Net debt is simply gross debt less liquid financial assets, which mainly consist of foreign exchange reserves and cash deposits. Net borrowing is the headline measure of the sector’s deficit and is based on when expenditures and receipts (largely taxation) are recorded rather than when cash is actually paid or received. (Click  The ratcheting up of debt levels affects debt servicing costs and hence the budgetary position of government. Yet the recent increases in interest rates also raise the costs faced by governments in financing future deficits or refinancing existing debts that are due to mature. In addition, a continuation of the low economic growth that has beset the UK economy since the global financial crisis also has implications for the burden imposed on the public sector by its debts, and hence the sustainability of the public finances. After all, low growth has implications for spending commitments, and, of course, the flow of receipts.
The ratcheting up of debt levels affects debt servicing costs and hence the budgetary position of government. Yet the recent increases in interest rates also raise the costs faced by governments in financing future deficits or refinancing existing debts that are due to mature. In addition, a continuation of the low economic growth that has beset the UK economy since the global financial crisis also has implications for the burden imposed on the public sector by its debts, and hence the sustainability of the public finances. After all, low growth has implications for spending commitments, and, of course, the flow of receipts. 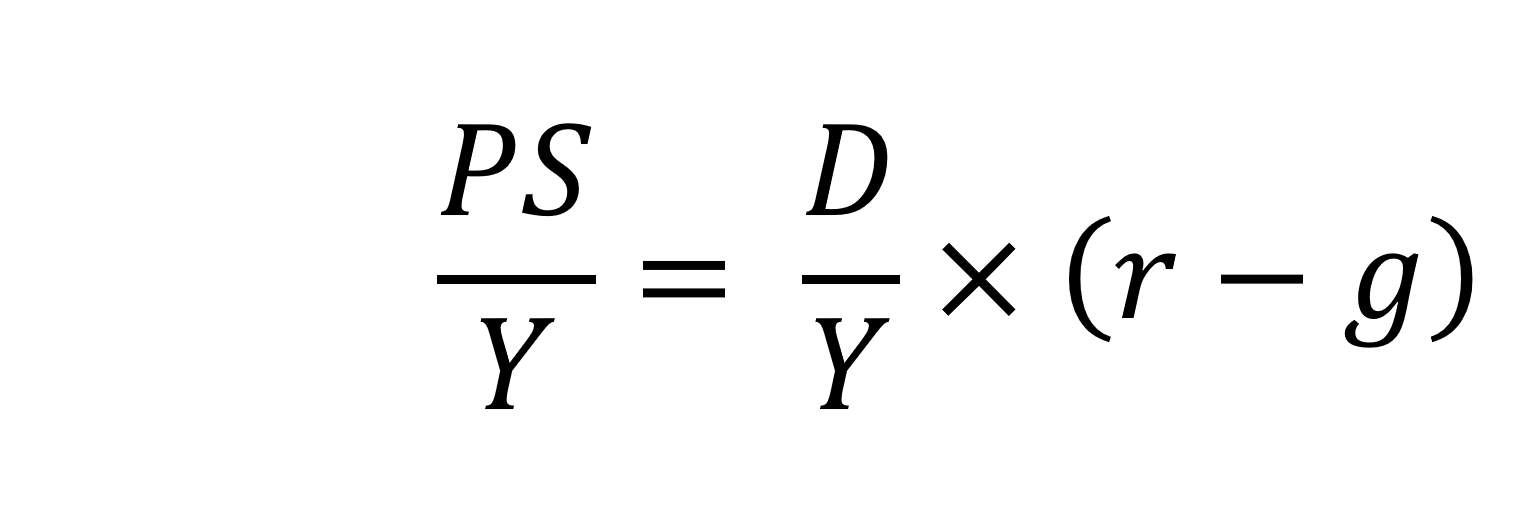
 Consider Charts 2 and 3 to understand how the ‘r – g’ differential has affected debt sustainability in the UK since 1990. Chart 2 plots the implied yield on 10-year government bonds, alongside the annual rate of nominal growth (click
Consider Charts 2 and 3 to understand how the ‘r – g’ differential has affected debt sustainability in the UK since 1990. Chart 2 plots the implied yield on 10-year government bonds, alongside the annual rate of nominal growth (click  Chart 3 plots the ‘r – g’ differential which is simply the difference between the two series in Chart 2, along with a 12-month rolling average of the differential to help show better the direction of the differential by smoothing out some of the short-term volatility (click
Chart 3 plots the ‘r – g’ differential which is simply the difference between the two series in Chart 2, along with a 12-month rolling average of the differential to help show better the direction of the differential by smoothing out some of the short-term volatility (click  Yet the negative differential resumed in 2010 and continued up to the pandemic. Again, this is indicative of the macroeconomic and financial environments being supportive of the public finances. It was, however, largely driven by low interest rates rather than by economic growth.
Yet the negative differential resumed in 2010 and continued up to the pandemic. Again, this is indicative of the macroeconomic and financial environments being supportive of the public finances. It was, however, largely driven by low interest rates rather than by economic growth.  The pandemic saw the ‘r – g’ differential again turn markedly positive, averaging 7 percentage points in the four quarters from Q2 of 2020. While the differential again turned negative, the debt-to-GDP ratio had also increased substantially because of large-scale fiscal interventions. This made the negative differential even more important for the sustainability of the public finances. The question is how long the negative differential can last.
The pandemic saw the ‘r – g’ differential again turn markedly positive, averaging 7 percentage points in the four quarters from Q2 of 2020. While the differential again turned negative, the debt-to-GDP ratio had also increased substantially because of large-scale fiscal interventions. This made the negative differential even more important for the sustainability of the public finances. The question is how long the negative differential can last. In his blog,
In his blog,  Discretionary fiscal measures in the UK are usually announced in annual Budget statements in the House of Commons. These are normally in March, but discretionary fiscal changes can be made in the Autumn Statement too. The Autumn Statement of October 2022, for example, took on significant importance as the new Chancellor of the Exchequer, Jeremy Hunt, tried to present a ‘safe pair hands’ following the fallout and market turbulence in response to the fiscal statement by the former Chancellor, Kwasi Kwarteng, on 23 September that year.
Discretionary fiscal measures in the UK are usually announced in annual Budget statements in the House of Commons. These are normally in March, but discretionary fiscal changes can be made in the Autumn Statement too. The Autumn Statement of October 2022, for example, took on significant importance as the new Chancellor of the Exchequer, Jeremy Hunt, tried to present a ‘safe pair hands’ following the fallout and market turbulence in response to the fiscal statement by the former Chancellor, Kwasi Kwarteng, on 23 September that year. The size of discretionary fiscal interventions can be measured by the fiscal impulse. This captures the magnitude of change in discretionary fiscal policy and thus the size of the stimulus. The concept is not to be confused with fiscal multipliers, which measure the impact of fiscal changes on economic outcomes, such as real national income and employment.
The size of discretionary fiscal interventions can be measured by the fiscal impulse. This captures the magnitude of change in discretionary fiscal policy and thus the size of the stimulus. The concept is not to be confused with fiscal multipliers, which measure the impact of fiscal changes on economic outcomes, such as real national income and employment.  A primary deficit captures the extent to which the receipts of the public sector fall short of its spending, excluding its spending on debt interest payments. It essentially captures whether the public sector is able to afford its ‘new’ fiscal choices from its receipts; it excludes debt-servicing costs, which can be thought of as reflecting fiscal choices of the past. By using a cyclically-adjusted primary deficit we are able to isolate more accurately the size of discretionary policy changes. Chart 1 shows the UK’s actual and cyclically-adjusted primary deficit as a share of GDP since 1975, which have averaged 1.3 and 1.1 per cent of GDP respectively. (Click
A primary deficit captures the extent to which the receipts of the public sector fall short of its spending, excluding its spending on debt interest payments. It essentially captures whether the public sector is able to afford its ‘new’ fiscal choices from its receipts; it excludes debt-servicing costs, which can be thought of as reflecting fiscal choices of the past. By using a cyclically-adjusted primary deficit we are able to isolate more accurately the size of discretionary policy changes. Chart 1 shows the UK’s actual and cyclically-adjusted primary deficit as a share of GDP since 1975, which have averaged 1.3 and 1.1 per cent of GDP respectively. (Click  Chart 2 shows the magnitude of UK fiscal impulses since 1980. It captures very starkly the extent of the loosening of the fiscal stance in 2020 in response to the COVID-19 pandemic. (Click
Chart 2 shows the magnitude of UK fiscal impulses since 1980. It captures very starkly the extent of the loosening of the fiscal stance in 2020 in response to the COVID-19 pandemic. (Click  Over the decades, economies have become increasingly interdependent. This process of globalisation has involved a growth in international trade, the spread of technology, integrated financial markets and international migration.
Over the decades, economies have become increasingly interdependent. This process of globalisation has involved a growth in international trade, the spread of technology, integrated financial markets and international migration. According to the Office for Budget Responsibility’s November 2022 Economic and Fiscal Outlook, Brexit will result in the UK’s trade intensity being 15 per cent lower in the long run than if it had remained in the EU.
According to the Office for Budget Responsibility’s November 2022 Economic and Fiscal Outlook, Brexit will result in the UK’s trade intensity being 15 per cent lower in the long run than if it had remained in the EU.  But trade can increase dependence on unreliable supply sources. For example, at present, some companies are seeking to reduce their reliance on Taiwanese parts, given worries about possible Chinese actions against Taiwan.
But trade can increase dependence on unreliable supply sources. For example, at present, some companies are seeking to reduce their reliance on Taiwanese parts, given worries about possible Chinese actions against Taiwan.  The problems with a globally interdependent world have led to world trade growing more slowly than world GDP in recent years after decades of trade growth considerably outstripping GDP growth. Trade (imports plus exports) as a percentage of GDP peaked at just over 60% in 2008. In 2019 and 2021 it was just over 56%. This is illustrated in the chart (click
The problems with a globally interdependent world have led to world trade growing more slowly than world GDP in recent years after decades of trade growth considerably outstripping GDP growth. Trade (imports plus exports) as a percentage of GDP peaked at just over 60% in 2008. In 2019 and 2021 it was just over 56%. This is illustrated in the chart (click 