 In a blog from March 2023 (reproduced below), we saw how there has been growing pressure around the world for employers to move to a four-day week. Increasing numbers of companies have adopted the model of 80% of the hours for 100% of the pay.
In a blog from March 2023 (reproduced below), we saw how there has been growing pressure around the world for employers to move to a four-day week. Increasing numbers of companies have adopted the model of 80% of the hours for 100% of the pay.
As we see below, the model adopted has varied across companies, depending on what was seen as most suitable for them. Some give everyone Friday off; others let staff choose which day to have off; others let staff work 80% of the hours on a flexible basis. Firms adopting the model have generally found that productivity and revenue have increased, as has employee well-being. To date, over 200 employers in the UK, employing more than 5000 people, have adopted a permanent four-day week.
This concept of 100-80-100, namely 100% of pay for 80% of hours, but 100% of output, has been trialled in several countries. In Germany, after trials over 2024, 73% of the companies involved plan to continue with the new model, with the remaining 27% either making minor tweaks or yet to decide. Generally hourly productivity rose, and in many cases total output also rose. As the fourth article below states:
The primary causal factor for this intriguing revelation was simple – efficiency became the priority. Reports from the trial showed that the frequency and duration of meetings was reduced by 60%, which makes sense to anyone who works in an office – many meetings could have been a simple email. 25% of companies tested introduced new digitised ways of managing their workflow to optimise efficiency.
Original post
In two previous posts, one at the end of 2019 and one in July 2021, we looked at moves around the world to introduce a four-day working week, with no increase in hours on the days worked and no reduction in weekly pay. Firms would gain if increased worker energy and motivation resulted in a gain in output. They would also gain if fewer hours resulted in lower costs.
Workers would be likely to gain from less stress and burnout and a better work–life balance. What is more, firms’ and workers’ carbon footprint could be reduced as less time was spent at work and in commuting.
If the same output could be produced with fewer hours worked, this would represent an increase in labour productivity measured in output per hour.
The UK’s poor productivity record since 2008
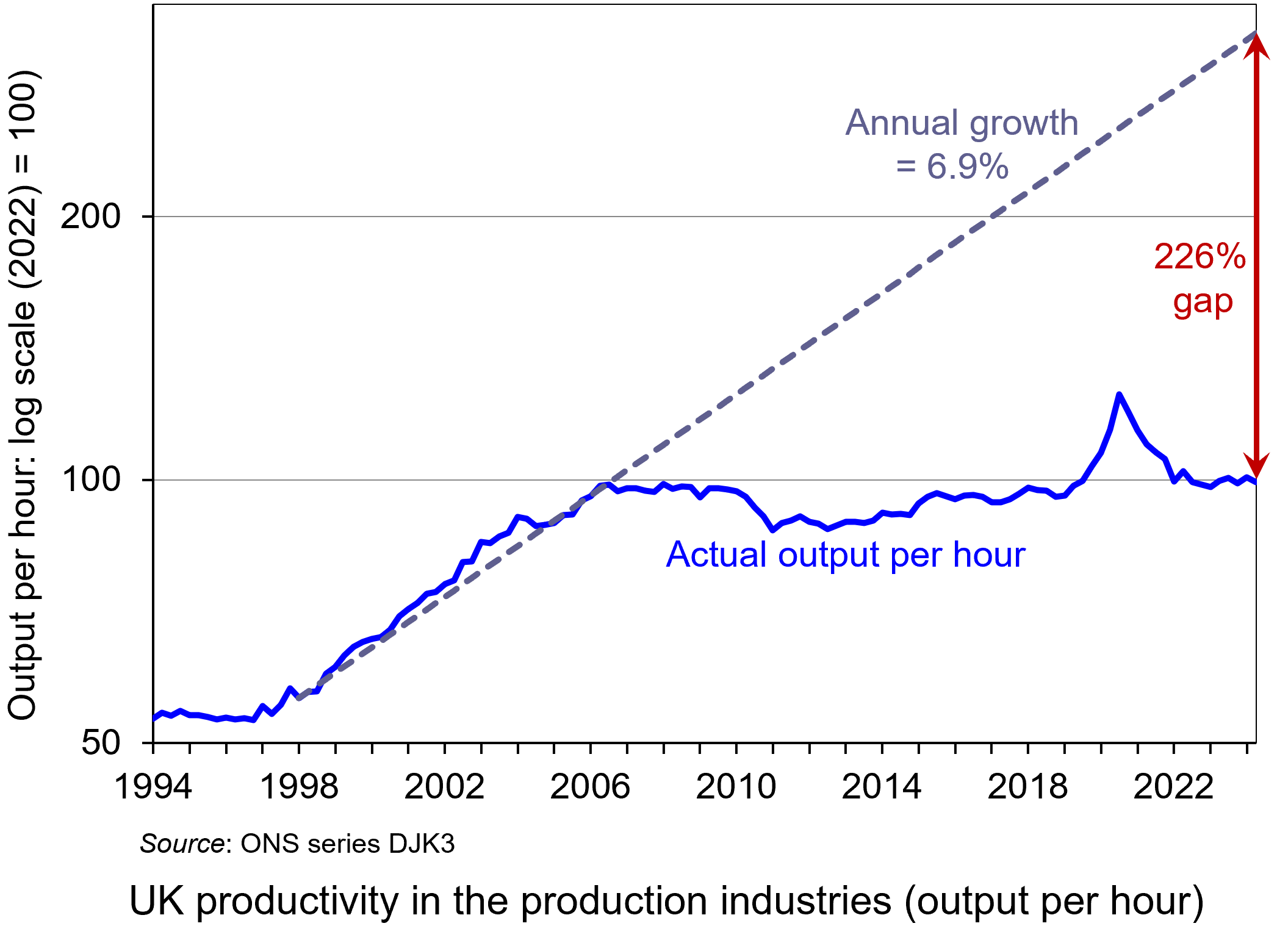 Since the financial crisis of 2007–8, the growth in UK productivity has been sluggish. This is illustrated in the chart, which looks at the production industries: i.e. it excludes services, where average productivity growth tends to be slower. The chart has been updated to 2024 Q2 – the latest data available. (Click here for a PowerPoint of the chart.)
Since the financial crisis of 2007–8, the growth in UK productivity has been sluggish. This is illustrated in the chart, which looks at the production industries: i.e. it excludes services, where average productivity growth tends to be slower. The chart has been updated to 2024 Q2 – the latest data available. (Click here for a PowerPoint of the chart.)
Prior to the crisis, from 1998 to 2006, UK productivity in the production industries grew at an annual rate of 6.9%. From 2007 to the start of the pandemic in 2020, the average annual productivity growth rate in these industries was a mere 0.2%.
It grew rapidly for a short time at the start of the pandemic, but this was because many businesses temporarily shut down or went to part-time working, and many of these temporary job cuts were low-wage/low productivity jobs. If you take services, the effect was even stronger as sectors such as hospitality, leisure and retail were particularly affected and labour productivity in these sectors tends to be low. As industries opened up and took on more workers, so average productivity rapidly fell back. Since then productivity has flatlined.
If you project the average productivity growth rate from 1998 to 2007 of 6.9% forwards (see grey dashed line), then by 2024 Q3, output per hour in the production industries would have been 3.26 times higher than it actually was: a gap of 226%. This is a huge productivity gap.
 Productivity in the UK is lower than in many other competitor countries. According to the ONS, output per hour in the UK in 2021 was $59.14 in the UK. This compares with an average of $64.93 for the G7 countries, $66.75 in France, £68.30 in Germany, $74.84 in the USA, $84.46 in Norway and $128.21 in Ireland. It is lower, however, in Italy ($54.59), Canada ($53.97) and Japan ($47.28).
Productivity in the UK is lower than in many other competitor countries. According to the ONS, output per hour in the UK in 2021 was $59.14 in the UK. This compares with an average of $64.93 for the G7 countries, $66.75 in France, £68.30 in Germany, $74.84 in the USA, $84.46 in Norway and $128.21 in Ireland. It is lower, however, in Italy ($54.59), Canada ($53.97) and Japan ($47.28).
As we saw in the blog, The UK’s poor productivity record, low UK productivity is caused by a number of factors, not least the lack of investment in physical capital, both by private companies and in public infrastructure, and the lack of investment in training. Other factors include short-termist attitudes of both politicians and management and generally poor management practices. But one cause is the poor motivation of many workers and the feeling of being overworked. One solution to this is the four-day week.
Latest evidence on the four-day week
Results have just been released of a pilot programme involving 61 companies and non-profit organisations in the UK and nearly 3000 workers. They took part in a six-month trial of a four-day week, with no increase in hours on the days worked and no loss in pay for employees – in other words, 100% of the pay for 80% of the time. The trial was a success, with 91% of organisations planning to continue with the four-day week and a further 4% leaning towards doing so.
 The model adopted varied across companies, depending on what was seen as most suitable for them. Some gave everyone Friday off; others let staff choose which day to have off; others let staff work 80% of the hours on a flexible basis.
The model adopted varied across companies, depending on what was seen as most suitable for them. Some gave everyone Friday off; others let staff choose which day to have off; others let staff work 80% of the hours on a flexible basis.
There was little difference in outcomes across different types of businesses. Compared with the same period last year, revenues rose by an average of 35%; sick days fell by two-thirds and 57% fewer staff left the firms. There were significant increases in well-being, with 39% saying they were less stressed, 40% that they were sleeping better; 75% that they had reduced levels of burnout and 54% that it was easier to achieve a good work–life balance. There were also positive environmental outcomes, with average commuting time falling by half an hour per week.
There is growing pressure around the world for employers to move to a four-day week and this pilot provides evidence that it significantly increases productivity and well-being.
Additional articles
Original set of articles
- Results from world’s largest 4 day week trial bring good news for the future of work
4 Day Week Global, Charlotte Lockhart (21/2/23)
- Four-day week: ‘major breakthrough’ as most UK firms in trial extend changes
The Guardian, Heather Stewart (21/2/23)
- Senedd committee backs four-day working week trial in Wales
The Guardian, Steven Morris (24/1/23)
- ‘Major breakthrough’: Most firms say they’ll stick with a four-day working week after successful trial
Sky News, Alice Porter (21/2/23)
- Major four-day week trial shows most companies see massive staff mental health benefits and profit increase
Independent, Anna Wise (21/2/23)
- Four-day week: Which countries have embraced it and how’s it going so far?
euronews, Josephine Joly and Luke Hurst (23/2/23)
- Firms stick to four-day week after trial ends
BBC News, Simon Read, Lucy Hooker & Emma Simpson (21/2/23)
- The climate benefits of a four-day workweek
BBC Future Planet, Giada Ferraglioni and Sergio Colombo (21/2/23)
- Four-day working week: why UK businesses and workers will continue with new work pattern, plus pros and cons
National World, Rochelle Barrand (22/2/23)
- Most companies in UK four-day week trial to continue with flexible working
Financial Times, Daniel Thomas and Emma Jacobs (21/2/23)
- The pros and cons of a four-day working week
Financial Times, Editorial (13/2/23)
- Explaining the UK’s productivity slowdown: Views of leading economists
VoxEU, Ethan Ilzetzki (11/3/20)
- Why the promised fourth industrial revolution hasn’t happened yet
The Conversation, Richard Markoff and Ralf Seifert (27/2/23)
Questions
- What are the possible advantages of moving to a four-day week?
- What are the possible disadvantages of moving to a four-day week?
- What types of companies or organisations are (a) most likely, (b) least likely to gain from a four-day week?
- Why has the UK’s productivity growth been lower than that of many of its major competitors?
- Why, if you use a log scale on the vertical axis, is a constant rate of growth shown as a straight line? What would a constant rate of growth line look like if you used a normal arithmetical scale for the vertical axis?
- Find out what is meant by the ‘fourth industrial revolution’. Does this hold out the hope of significant productivity improvements in the near future? (See, for example, last link above.)
 On the day he came to office, President Trump signed a series of executive orders. One of these was to set in motion the process of withdrawing from the UN Paris climate agreement. Section 3(a) of the order reads:
On the day he came to office, President Trump signed a series of executive orders. One of these was to set in motion the process of withdrawing from the UN Paris climate agreement. Section 3(a) of the order reads:
The United States Ambassador to the United Nations shall immediately submit formal written notification of the United States’ withdrawal from the Paris Agreement under the United Nations Framework Convention on Climate Change.
The Paris Agreement is an international treaty on climate change. It was adopted on 12 December 2015 and came into force on 4 November 2016, 30 days after the point was reached when at least 55 countries accounting for at least 55% of global emissions had ratified the treaty.
Currently, all UN countries are signatories to the agreement and only Iran, Libya and Yemen are yet to ratify it. The agreement commits countries to limiting global warming to well under 2°C above pre-industrial levels and preferably to no more than 1.5°C. This would involve reducing greenhouse gas emissions and/or taking carbon absorbing measures.
 Since 2020, each country has been required to submit its own emission-reduction targets, known as ‘nationally determined contributions’ (NDCs), and the actions it will take to meet them. Every five years each country must submit a new NDC more ambitious than the last.
Since 2020, each country has been required to submit its own emission-reduction targets, known as ‘nationally determined contributions’ (NDCs), and the actions it will take to meet them. Every five years each country must submit a new NDC more ambitious than the last.
Rich countries are expected to provide finance to low-income countries. This is required to help poor countries adopt green technologies and to adapt to the harmful effects of climate change (e.g. through irrigation schemes and flood defences).
Countries set target dates by which emissions would be fully offset by carbon absorption measures (‘net zero’). The UN’s goal is to reach global net zero by 2050. According to the UN Climate Action site:
As of June 2024, 107 countries, responsible for approximately 82 per cent of global greenhouse gas emissions, had adopted net-zero pledges either in law, in a policy document such as an national climate action plan or a long-term strategy, or in an announcement by a high-level government official. More than 9000 companies, over 1000 cities, more than 1000 educational institutions, and over 600 financial institutions have joined the Race to Zero, pledging to take rigorous, immediate action to halve global emissions by 2030.
The Paris Agreement has helped to cut emissions or slow their rate of growth in most countries. Although net zero by 2050 may be unlikely, warming will be less than without the agreement.
The USA and the Paris Agreement
 In April 2016 the USA signed the Paris Agreement. As stated above, the Paris Agreement came into effect on 4 November 2016.
In April 2016 the USA signed the Paris Agreement. As stated above, the Paris Agreement came into effect on 4 November 2016.
President Trump came to office for the first time in January 2017. In June 2017, he signed an executive order in which he announced that the USA would withdraw from the agreement, arguing that it undermined the US economy and put it at a competitive disadvantage. He claimed that global warming is a hoax concocted by China designed to undermine the competitive power of the USA.
However, despite Trump’s intention to withdraw from the agreement, its terms did not allow a country to begin a withdrawal procedure for at least three years after the agreement was ratified (i.e. not before 4 November 2019) and then a year’s notice has to be given. This notice was given on 4 November 2019. In the meantime, the USA had to abide by the terms of the treaty. During this period, US representatives at COP meetings used the opportunity to promote fossil fuels. Withdrawal took place on 1 November 2020, just one day after the presidential election and just over two months before the end of Trump’s first term of office.
On 20 January 2021, his first day in office, President Biden signed an executive order to rejoin the agreement, which took place on 19 February 2021. He committed to cutting total greenhouse gas emissions by at least 50% by 2030. To achieve this, his administration adopted a number of emissions-reducing measures, for example requiring all new passenger vehicles sold after 2035 to be emissions free, giving tax credits for clean electricity generation, providing federal funds for smart agriculture and setting greener appliance and equipment standards.
But, as we have seen, newly elected President Trump for the second time announced that the USA would withdraw from the Paris agreement and would prioritise fossil fuel production, under the mantra, ‘drill, baby, drill’.
The economics of climate change
 Climate change is directly caused by market failures. One of the most important of these is that the atmosphere is a common resource: it is not privately owned; it is a global ‘commons’. Individuals and firms use it at a zero price. If the price of any good or service to the user is zero, there is no incentive to economise on its use. Thus for the emitter there are no private costs of using the atmosphere in this way as a ‘dump’ for their emissions and, in a free market, no incentive to reduce the climate costs.
Climate change is directly caused by market failures. One of the most important of these is that the atmosphere is a common resource: it is not privately owned; it is a global ‘commons’. Individuals and firms use it at a zero price. If the price of any good or service to the user is zero, there is no incentive to economise on its use. Thus for the emitter there are no private costs of using the atmosphere in this way as a ‘dump’ for their emissions and, in a free market, no incentive to reduce the climate costs.
And yet when firms emit greenhouse gases into the atmosphere there are costs to other people. To the extent that they contribute to global warming, part of these costs will be borne by the residents of that country; but a large part will be borne by inhabitants of other countries.
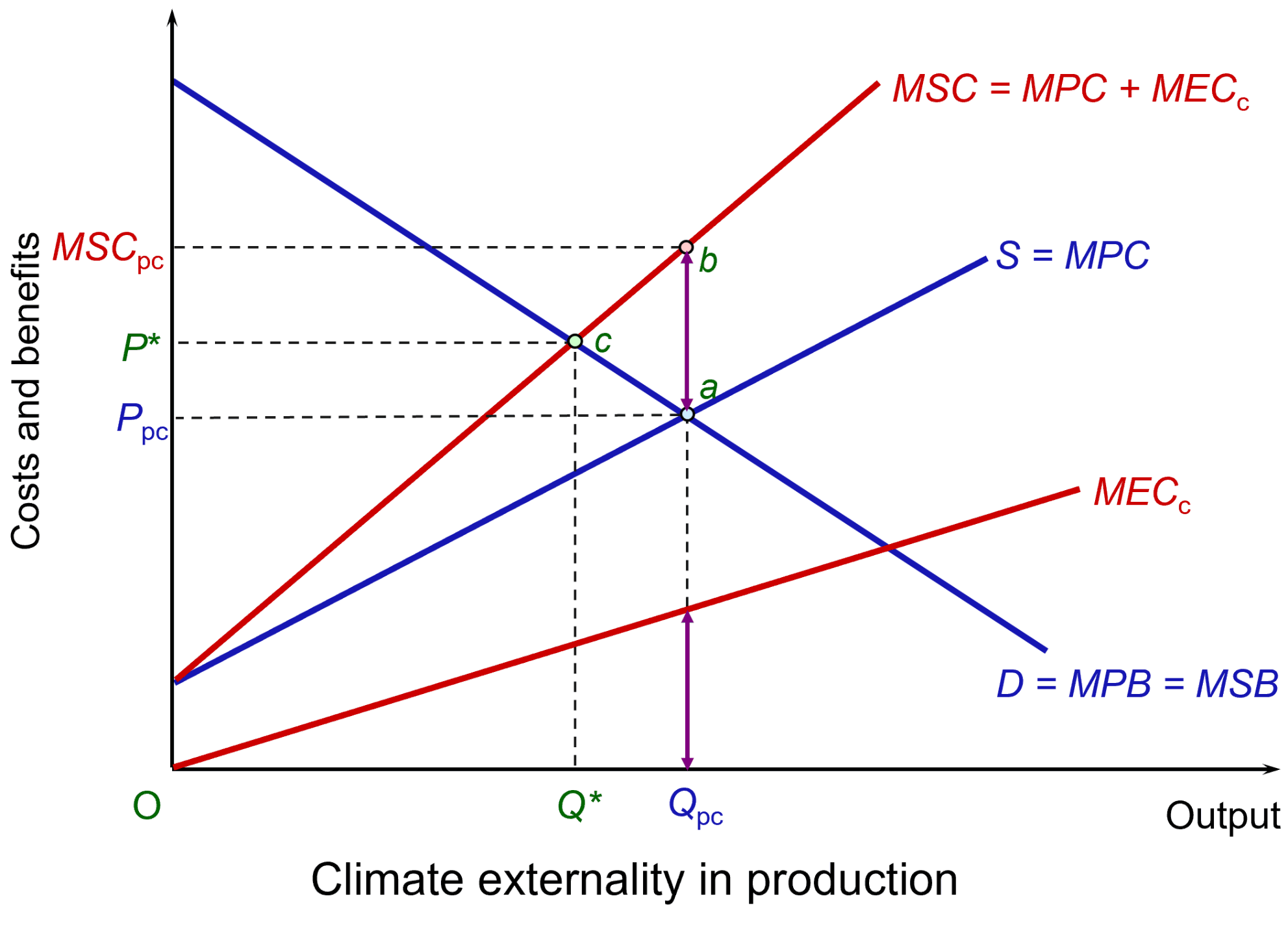 These climate costs are external costs to the firm and are illustrated in the figure. It shows an industry that emits CO2. To keep the analysis simple, assume that it is a perfectly competitive industry with demand and supply given by curves D and S, which are equal to the marginal private benefits (MPB) and marginal private costs (MPC), respectively. There are no externalities on the demand side and hence MPB equals the marginal social cost (MSB). Market equilibrium is at point a, with output at Qpc and price at Ppc. (Click here for a PowerPoint.)
These climate costs are external costs to the firm and are illustrated in the figure. It shows an industry that emits CO2. To keep the analysis simple, assume that it is a perfectly competitive industry with demand and supply given by curves D and S, which are equal to the marginal private benefits (MPB) and marginal private costs (MPC), respectively. There are no externalities on the demand side and hence MPB equals the marginal social cost (MSB). Market equilibrium is at point a, with output at Qpc and price at Ppc. (Click here for a PowerPoint.)
Assume that the emissions create a marginal cost to society equal to MECc. Assume that the MEC increases as output and total emissions increase. The MECc line is thus upward sloping. At the market price of Qpc, these external climate costs are equal to the purple vertical line. When these external climate costs are added to private costs, this gives a marginal social cost given by MSC = MPC + MECc. The gives a socially optimal level of output of the product of Q* at a price of P*, with the optimum point of c.
 In other words, other things being equal, the free market overproduces products with climate externalities. If the output is to be reduced to the social optimum of Q*, then the government will need to take measures such as those advocated in the Paris Agreement. These could include imposing taxes on products, such as electricity generated by fossil fuels, or on the emissions themselves. Or green alternatives, such as wind power, could be subsidised.
In other words, other things being equal, the free market overproduces products with climate externalities. If the output is to be reduced to the social optimum of Q*, then the government will need to take measures such as those advocated in the Paris Agreement. These could include imposing taxes on products, such as electricity generated by fossil fuels, or on the emissions themselves. Or green alternatives, such as wind power, could be subsidised.
Alternatively, regulations could be used to cap the production of products creating emissions, or caps on the emissions themselves could be imposed. Emissions permits could be issued or auctioned. Only firms in possession of the permits would be allowed to emit and the permits would cap emissions below free-market levels. These permits could be traded under a cap-and-trade scheme, such as the EU’s Emissions Trading Scheme. Again, such schemes are advocated under the Paris Agreement.
Effect of the USA’s withdrawal from the Paris Agreement
 Withdrawal from the Paris Agreement and promoting fossil fuels will increase US emissions. Scientific consensus is that this will have a negative effect on climate change. Only part of these climate costs will be borne by the USA, although the severity of recent fires in California, fanned by strong Santa Ana winds, and more violent hurricanes are two examples of costs of climate change to the USA itself.
Withdrawal from the Paris Agreement and promoting fossil fuels will increase US emissions. Scientific consensus is that this will have a negative effect on climate change. Only part of these climate costs will be borne by the USA, although the severity of recent fires in California, fanned by strong Santa Ana winds, and more violent hurricanes are two examples of costs of climate change to the USA itself.
A bigger worry is whether the USA’s withdrawal will encourage other countries, such as Argentina, to do likewise. Then the climate costs of US withdrawal will be greater.
But all is not bad news. The transition to green energy is well advanced and the costs of solar and wind power are decreasing. Global investment in clean energy has increased by 60% since 2015. China is investing heavily in renewable energy technology, which is giving it a significant trade advantage. The EU has taken significant actions to promote green energy and technology. Similarly, industrial processes that economise on emissions are developing apace and it is becoming increasingly profitable for private companies to make climate-friendly investments without subsidies. In the USA itself, many Democratic states and local governments, and even some Republican ones, will continue to adopt climate-friendly policies.
In this environment, the Trump administration does not want to fall behind in the development of new technologies and markets. And with Elon Musk having a significant influence on Donald Trump, the USA’s investment in EVs and battery technology is likely to continue. This will help to reduce the price of green energy and transport.
Videos
Articles
- Trump vows to leave Paris climate agreement and ‘drill, baby, drill’
BBC News, Matt McGrath (20/1/25)
- What is the Paris climate agreement and why has Trump withdrawn?
BBC News, Esme Stallard and Mark Poynting (21/1/25)
- Six Trump executive orders to watch
BBC News (21/1/25)
- The real message behind Trump’s withdrawal of US from the Paris climate agreement
Sky News, Tom Clarke (21/1/25)
- Trump signs order to withdraw US from Paris climate agreement for second time
The Guardian, Dharna Noor (20/1/25)
- Explained: how Trump’s day one orders reveal a White House for big oi
The Guardian, Oliver Milman and Dharna Noor (22/1/25)
- Donald Trump can’t stop global climate action. If we stick together, it’s the US that will lose out
The Guardian, Bill Hare (6/11/24)
 Trump to pull US from Paris climate agreement: What could this mean for the environment?
Trump to pull US from Paris climate agreement: What could this mean for the environment?ITV News, Martin Stew (21/1/25)
- 10 reasons why US president-elect Donald Trump can’t derail global climate action
The Conversation, Wesley Morgan and Ben Newell (8/11/24)
- Trump has rejected the Paris agreement again, but game theory shows how other countries can still lead by example
The Conversation, Renaud Foucart (27/1/25)
Information
Questions
- Summarise the Paris Agreement.
- Using a diagram similar to that above, illustrate how the free market will produce a sub-optimal amount of solar power because the marginal social benefit exceeds the marginal private benefit.
- How might game theory be used to analyse possible international decision making in the context of US climate policy?
- Is it in America’s interests to cease investing in green energy and green production methods?
- Go through each of the reasons (not specific to Australia) given in The Conversation article linked above why ‘Donald Trump can’t derail global climate action’. To what extent do you agree with each one?
 The election of Donald Trump saw the market price of bitcoin rise from $67 839 on election day (5 November 2024) to £106 168 on 18 December: a rise of 56%. It was $104 441 the day before inauguration (20 January 2025).
The election of Donald Trump saw the market price of bitcoin rise from $67 839 on election day (5 November 2024) to £106 168 on 18 December: a rise of 56%. It was $104 441 the day before inauguration (20 January 2025).
Trump has been a keen supporter of cryptocurrencies. He has stated that he wants the USA to become the world’s ‘crypto capital’. Indeed, he and Melania Trump have launched their own meme coins hosted on the Solana blockchain. Meme coins are tokens, a form of cryptocurrency, inspired by specific individuals, characters, cartoons or artwork.
On 23 January, three days after his inauguration, President Trump signed an Executive Order. This states that it is:
…the policy of my Administration to support the responsible growth and use of digital assets, blockchain technology, and related technologies across all sectors of the economy, including by … protecting and promoting the ability of individual citizens and private-sector entities alike to access and use for lawful purposes open public blockchain networks without persecution, including the ability to develop and deploy software, to participate in mining and validating, to transact with other persons without unlawful censorship, and to maintain self-custody of digital assets…
The full Executive Order can be read here.
Cryptocurrencies
Although cryptocurrencies can be used for certain transactions and avoid the need for banks, their use as a medium of exchange or unit of account is limited by their price volatility. The supply of national or regional currencies, such as the US dollar, the euro and the pound sterling is controlled by central banks, and central banks have a key mandate of achieving price stability, where price is in terms of their currency’s consumer price index. Although exchange rates fluctuate and thereby affect the prices of internationally traded goods and assets, such fluctuations are small in comparison with crypto price fluctuations.
 The supply of many cryptocurrencies is not controlled with the objective of achieving price stability. Indeed, certain cryptocurrencies, such as bitcoin (the coins with the highest total market value of approximately $2060bn) have a limited maximum supply. The supply of bitcoin in January 2025 is officially 19.81m, 94.3% of the eventual official total of 21m. However, with some 1.8m coins lost, the current effective total supply is more like 18m and the ceiling 19.2m. New coins are created by ‘mining’, involving massive computer power to perform complex calculations. Coins in circulation at any one time are therefore fixed and increase only slowly and at a decelerating rate over time, with increased mining costs per coin. On any one day, however, the supply offered for sale can fluctuate wildly.
The supply of many cryptocurrencies is not controlled with the objective of achieving price stability. Indeed, certain cryptocurrencies, such as bitcoin (the coins with the highest total market value of approximately $2060bn) have a limited maximum supply. The supply of bitcoin in January 2025 is officially 19.81m, 94.3% of the eventual official total of 21m. However, with some 1.8m coins lost, the current effective total supply is more like 18m and the ceiling 19.2m. New coins are created by ‘mining’, involving massive computer power to perform complex calculations. Coins in circulation at any one time are therefore fixed and increase only slowly and at a decelerating rate over time, with increased mining costs per coin. On any one day, however, the supply offered for sale can fluctuate wildly.
Some other crypto currencies also have a long-term supply ceiling and are created by mining. Others, such as ether (the coins with the second highest market value of approximately $394bn) do not have a fixed supply ceiling. They are not created by mining, but by a system known as ‘Proof-of-Stake (PoS)’. This uses the cryptocurrency’s owners, who stake some of their currency, to validate transactions on the Ethereum blockchain. They receive new ether as a reward. PoS uses considerably less energy than mining and hence is regarded as greener.
Unlike mined coins, Ethereum coins (ether) created by PoS can be ‘burned’: i.e. removed from circulating supply. This can more than offset new coins created and lead to a net decrease in supply. See the Fidelity Digital Assets and Paxful links below for a discussion of what determines the net burn/net creation rate of ether. Other coins, such as BNB (Binance’s cryptocurrency), have regular burns to control supply.
 There are some cryptocurrencies that are suitable as a medium of exchange and as a unit of value. These are ‘stablecoins’, whose value is linked 1:1 to a major currency, such as the US dollar or euro. Supply is adjusted to maintain this value. Stablecoins are used primarily for transactions. They account for some two-thirds of all transactions using crypto. They are particularly used for transactions in parts of the world with monetary instability and/or limited access to major currencies.
There are some cryptocurrencies that are suitable as a medium of exchange and as a unit of value. These are ‘stablecoins’, whose value is linked 1:1 to a major currency, such as the US dollar or euro. Supply is adjusted to maintain this value. Stablecoins are used primarily for transactions. They account for some two-thirds of all transactions using crypto. They are particularly used for transactions in parts of the world with monetary instability and/or limited access to major currencies.
With the exception of stablecoins, crypto currencies are best seen as assets, rather than as a means of exchange or unit of account. As such, they are more comparable to gold than to conventional currencies.
The market for crypto in the long term
The market price of cryptocurrencies is determined by supply and demand. With limited supply, their price is likely to increase as demand is forecast to increase relative to supply. This is particularly the case with mined cryptocurrencies where there is a ceiling to supply. But even with PoS-created currencies, the amount supplied is likely to increase more slowly than demand, especially with burn mechanisms in place.
With many countries recognising and embracing cryptocurrencies as an asset, so the long-term price should rise. The endorsement by Donald Trump is likely to hasten this process.
The market for crypto in the short term
While the total supply of cryptocurrency is limited, the supply to market can fluctuate wildly, as can demand. This can cause huge gyrations in price.
Short-run demand and supply decisions are governed largely by expectations of future price changes, over anything from the next few hours to the coming months. If people think the price will rise, people will demand more, while those already holding crypto and thinking of selling will hold back. These actions will amplify the very effect they had predicted, namely a rise in price.
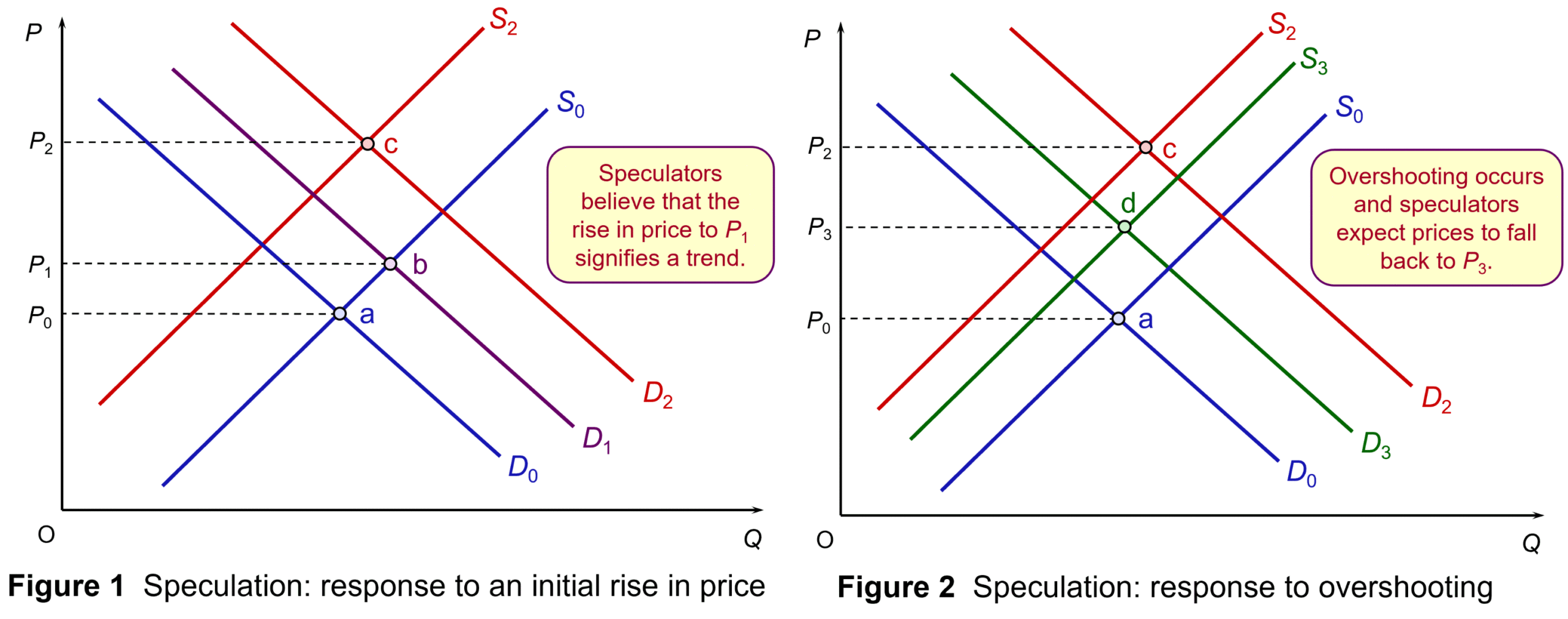
This is illustrated in Figure 1. Assume an initial rise in demand for a particular cryptocurrency from D0 to D1. Equilibrium moves from point a to point b and the price of the cryptocurrency rises from P0 to P1. Speculators believe that this is a trend and that prices will rise further. Demand increases to D2 as purchasers rush to buy; and supply falls to S2 as potential sellers of the crypto hold back. Equilibrium moves to point c and price rises to P2.
But in their exuberance, people may have pushed the price above the level that reflects underlying demand and supply. People respond to this overshooting by selling some of the currency to take advantage of what they see as a temporary high price. In Figure 2, supply rises from S2 to S3. Meanwhile, potential purchasers wait until price has settled back somewhat. Demand falls from D2 to D3. Equilibrium moves to point d, with price falling to P3. (Click here for a PowerPoint of the two diagrams.)

A similar process of speculation takes place when people expect prices to fall, with price potentially plummeting before it then recovers somewhat.
With computer algorithms interpreting underlying economic/political data, the price changes are likely to be frequent, with speculation amplifying these changes.
Articles
- Trump orders crypto working group to draft new regulations, explore national stockpile
Reuters, Hannah Lang and Trevor Hunnicutt (24/1/25)
- Bitcoin soars past $109,000 ahead of possible early action on crypto by Trump
MSN, Alan Suderman (20/1/25)
- 3 Things to Watch as Trump Becomes Memecoin Billionaire and US President
PYMNTS (20/1/25)
- Crypto Community Reacts to Trump and Melania Meme Coins as Market Sinks
Decrypt, Vismaya V (20/1/25)
- Trump’s plan for a strategic bitcoin reserve could trigger a crypto ‘arms race’ and reshape the global economic order
The Conversation, Huw Macartney, Erin McCracken and Robert Elliott (14/1/25)
- Bitcoin’s resurgence: A regulatory reset and a path to innovation
crypto.news, editorial (17/1/25)
- Bitcoin Retreats As Traders Await Trump Crypto Executive Order
Bloomberg on NDTV Profit (21/1/25)
- Bitcoin edges higher as investors shake off initial Trump Day One disappointment
Reuters, Tom Westbrook and Elizabeth Howcroft (21/1/25)
- Has bitcoin’s limited supply driven its rally? Experts weigh in
ABC News, Max Zahn (10/12/24)
Background information
Data
Questions
- What determines the supply of cryptocurrencies (a) in circulation; (b) to the market at any given time?
- Why are the prices of digital currencies so volatile?
- Why or why not are cryptocurrencies a good asset to hold?
- How may speculation (a) amplify and (b) dampen price fluctuations?
- What determines the net burn/net creation rate of ether?
- Should cryptocurrencies be classified as ‘money’?
 During the pandemic, most people who were not furloughed were forced to work from home. After lockdown restrictions were lifted, many employers decided to continue with people working remotely, at least for some of the time.
During the pandemic, most people who were not furloughed were forced to work from home. After lockdown restrictions were lifted, many employers decided to continue with people working remotely, at least for some of the time.
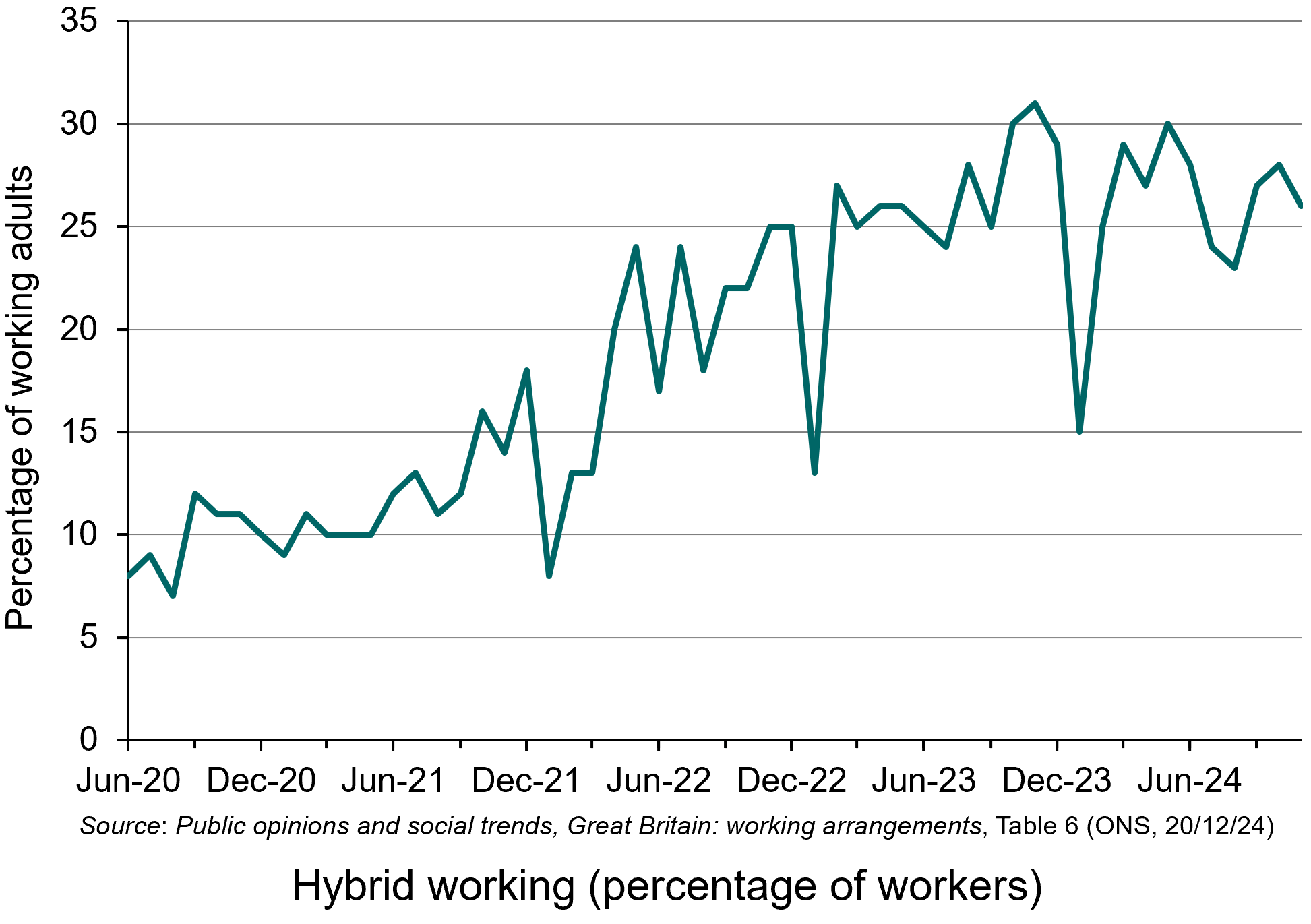
Today, this hybrid model, whereby workers work partly from home or local workspaces and partly in the office/factory/warehouse etc., has become the ‘new normal’ for around 26% of the working population in Great Britain – up from around 10% at the end of the national lockdowns in the Spring of 2021.
 Increasingly, however, employers who had introduced hybrid working are requiring their employees to return to the office, arguing that productivity and hence profits will rise as a result. Amazon is an example. Other employers, such as Asda, are increasing the time required in the office for hybrid workers.
Increasingly, however, employers who had introduced hybrid working are requiring their employees to return to the office, arguing that productivity and hence profits will rise as a result. Amazon is an example. Other employers, such as Asda, are increasing the time required in the office for hybrid workers.
Hybrid working had peaked at around 31% in November 2923 as the chart shows (click here for a PowerPoint). The chart is based on the December 20 database, Public opinions and social trends, Great Britain: working arrangements from the Office for National Statistics (see link under Data, below).
But why are some employers deciding that hybrid working is less profitable than working full time in the office. And does it apply to all employers and all employees or only certain types of firm and certain types of job?
The first thing to note is that hybrid work is more common among certain groups. These include older workers, parents, graduates and those with greater flexibility in scheduling their work, especially those in managerial or professional roles with greater flexibility. Certain types of work on the other hand do not lend themselves to hybrid work (or working completely from home, for that matter). Shop workers and those providing a direct service to customers, such as those working in the hospitality sector, cannot work remotely.
Benefits of hybrid working
For some employees and employers, hybrid working has brought significant benefits.
 For employees, less time and money is spent on commuting, which accounts for nearly an hour’s worth of the average worker’s daily time. According to the ONS survey, respondents spent an additional 24 minutes per day on sleep and rest and 15 minutes on exercise, sports and other activities that improved well-being compared to those who worked on-site. Working at home can make juggling work and home life easier, especially when workers can work flexible hours during the day, allowing them to fit work around family commitments.
For employees, less time and money is spent on commuting, which accounts for nearly an hour’s worth of the average worker’s daily time. According to the ONS survey, respondents spent an additional 24 minutes per day on sleep and rest and 15 minutes on exercise, sports and other activities that improved well-being compared to those who worked on-site. Working at home can make juggling work and home life easier, especially when workers can work flexible hours during the day, allowing them to fit work around family commitments.
Employers benefit from a healthier and more motivated staff who are more productive and less likely to quit. Hybrid work, being attractive to many workers, could allow employers to attract and retain talented workers. Also, employees may work longer hours if they are keen to complete a task and are not ‘clocking off’ at a particular time. Working from home allows workers to concentrate (unless distracted by other family members!).
By contrast, office working can be very inefficient, especially in open offices, where chatty colleagues can be distracting and it is difficult to concentrate. What is more, employees who are slightly unwell may continue working at home but may feel unable to commute to the office. If they did, they could spread their illness to other colleagues. Not allowing people to work from home can create a problem of ‘presenteeism’, where people feeling under the weather turn up to work but are unproductive.
One of the biggest benefits to employers of hybrid work is that costs can be saved by having smaller offices and by spending less on heating, lighting and facilities.
With hybrid working, time spent on site can be devoted to collaborative tasks, such as meetings with colleagues and customers/suppliers and joint projects where face-to-face discussion is required, or at least desirable. Tasks can also be completed that required specialist equipment or software not available at home.
Problems of hybrid working
So, if hybrid working has benefits for both employers and employees, why are some employers moving back to a system where employees work entirely on site?
 Some employers have found it hard to monitor and engage employees working from home. Workers may be easily distracted at home by other family members, especially if they don’t have a separate study/home office. People may feel detached from their co-workers on days they work from home. After a time, productivity may wane as workers find ways of minimising the amount of time actually working during declared work times.
Some employers have found it hard to monitor and engage employees working from home. Workers may be easily distracted at home by other family members, especially if they don’t have a separate study/home office. People may feel detached from their co-workers on days they work from home. After a time, productivity may wane as workers find ways of minimising the amount of time actually working during declared work times.
Far from improving work-life balance, for some workers the boundaries between work and personal life can become blurred, which can erode the value of personal and family time. This can create a feeling of never escaping from work and be demotivating and reduce productivity. Employees may stay logged on longer and work evenings and weekends in order to complete tasks.
Unless carefully planned, on days when people do go into the office they might not work effectively. They may be less likely to have profitable ad hoc conversations with co-workers, and meetings may be harder to arrange. Misunderstandings and miscommunication can occur when some employees are in the office but others are at home.
Some employers have found that the problems of hybrid working in their organisations have outweighed the benefits and that productivity has fallen. In justifying its ending of hybrid working from 1 January 2025, Amazon CEO, Andy Jessy, wrote in a memo to staff in September 2024:
To address the … issue of being better set up to invent, collaborate, and be connected enough to each other and our culture to deliver the absolute best for customers and the business, we’ve decided that we’re going to return to being in the office the way we were before the onset of COVID. When we look back over the last five years, we continue to believe that the advantages of being together in the office are significant.1
But is the solution to do as Amazon is doing and to abandon hybrid working and have a mass ‘return to the office’?
Improving hybrid working
There are ways of making hybrid working more effective so that the benefits can be maximised and the costs minimised.
Given that there are specific benefits from home working and other specific benefits from working on-site, it would be efficient to allocate time between home and office to maximise these benefits. The optimum balance is likely to vary from employer to employer, job to job and individual to individual.
 Where work needs to be done in teams and where team meetings are an important element of that work, it would generally make sense for such meetings to be held in person, especially when there needs to be a lot of discussion. If the team requires a brief catch up, however, this may be more efficiently done online via Teams or Zoom.
Where work needs to be done in teams and where team meetings are an important element of that work, it would generally make sense for such meetings to be held in person, especially when there needs to be a lot of discussion. If the team requires a brief catch up, however, this may be more efficiently done online via Teams or Zoom.
Individual tasks, on the other hand, which don’t require consultation with colleagues or the use of specific workplace facilities, are often carried out more efficiently when there is minimum chance of interruption. For many workers, this would be at home rather than in an office – especially an open-plan office. For others without a protected work space at home or nearby, it might be better to come into the office.
The conclusion is that managers need to think carefully about the optimum distribution between home and office working and accept that a one-size-fits-all model may not be optimum for all types of job and all workers. Recognising the relative benefits and costs of working in different venues and over different hours may help to achieve the best balance, both for employers and for workers. A crucial element here is the appropriate use of incentives. Workers need to be motivated. Sometimes this may require careful monitoring, but often a more hands-off approach by management, with the focus more on output and listening to the concerns of workers, rather than on time spent, may result in greater productivity.
1Message from CEO Andy Jassy: Strengthening our culture and teams, Amazon News (16/9/24)
Articles
- Hybrid working is the ‘new normal’, according to ONS
Personnel Today, Jo Faragher (11/11/24)
- Hybrid working is here to stay but needs better managing
Business Live, Dylan Jones-Evans (18/11/24)
- The permanently imperfect reality of hybrid work
BBC: Worklife, Alex Christian (11/12/23)
- The diminishing returns of in-office mandates
BBC: Worklife, Alex Christian (12/6/24)
- The Advantages and Challenges of Hybrid Work
Gallup: Workplace, Ben Wigert and Jessica White (14/9/22)
- 9 Challenges of hybrid working and how you should tackle them
Manager Talks, Ankita (10/3/24)
- 5 Challenges of Hybrid Work — and How to Overcome Them
Harvard Business Review, Martine Haas (15/2/22)
- Post-Christmas blues as UK bosses try to turn back clock on hybrid working
The Guardian, Joanna Partridge (3/1/25)
- ‘It didn’t come as a surprise’: UK workers on being forced back into the office
The Guardian, Rachel Obordo (3/1/25)
- Amazon tells staff to get back to office five days a week
BBC News, Natalie Sherman (16/9/24)
- Inequality in flexible working dividing Britain into ‘two-tier workforce’
The Guardian, Joanna Partridge (27/1/25)
Data
Questions
- Why may hybrid working be better for (a) employees and (b) employers than purely home working or purely working in the office?
- Why are many firms deciding that workers who were formerly employed on a hybrid basis should now work entirely from the office?
- What types of job are better performed on site, or with only a small amount of time working from home?
- What types of job are better performed by working at home with just occasional days in the office?
- Does the profile of workers (by age, qualifications, seniority, experience, family commitments, etc) affect the likelihood that they will work from home at least some of the time?
- How would you set about measuring the marginal productivity of a worker working from home? Is it harder than measuring the marginal productivity of the same worker doing the same job but working in the office?
- How may working in the office increase network effects?
- How may behavioural economics help managers to understand the optimum balance of home and on-site working?
 At an event at the London Palladium on 6 December staged to protest against elements in the recent Budget, the Conservative leader, Kemi Badenoch, was asked whether she would introduce a flat-rate income tax if the Conservatives were returned to government. She replied that it was a very attractive idea. But first the economy would need ‘rewiring’ so that the tax burden could be lightened.
At an event at the London Palladium on 6 December staged to protest against elements in the recent Budget, the Conservative leader, Kemi Badenoch, was asked whether she would introduce a flat-rate income tax if the Conservatives were returned to government. She replied that it was a very attractive idea. But first the economy would need ‘rewiring’ so that the tax burden could be lightened.
A flat-rate income tax system could take various forms, but the main feature is that there is a single rate of income tax. The specific rate would depend on how much the government wanted to raise. Also it could apply to just income tax, or to both income tax and social insurance (national insurance contributions (NICs) in the UK), or to income tax, social insurance and the withdrawal rate of social benefits. It could also apply to local/state taxes as well as national/federal taxes.
Take the simplest case of a flat-rate income tax with no personal allowance. In this system the marginal and average rate of tax is the same for everyone. This is known as a proportional tax.
Most countries have a progressive income tax system. This normally involves personal allowances (i.e. a zero rate up to a certain level of income) and then various tax bands, with the marginal rate rising when particular tax thresholds are reached. In England, Wales and Northern Ireland, there are three tax bands: 20%, 40% and 45%. Thus the higher a person’s income is, the higher their average rate of tax.
A regressive tax, by contrast, would be one where the average rate of tax fell as incomes rose. The extreme case of a regressive tax would be a lump-sum tax (such as a TV or other licence), which would be same absolute amount for everyone liable to it, irrespective of their income. This was the case with the ‘poll tax’ (or Community Charge, to give it its official title), introduced by Margaret Thatcher’s government in 1989 in Scotland and 1990 in the rest of the UK. It was a local tax, with each taxpayer taxed the same fixed sum, with the precise amount being set by each local authority. After protests and riots, it was replaced in 1993 by the current system of local taxation (Council Tax) based on property values in bands.
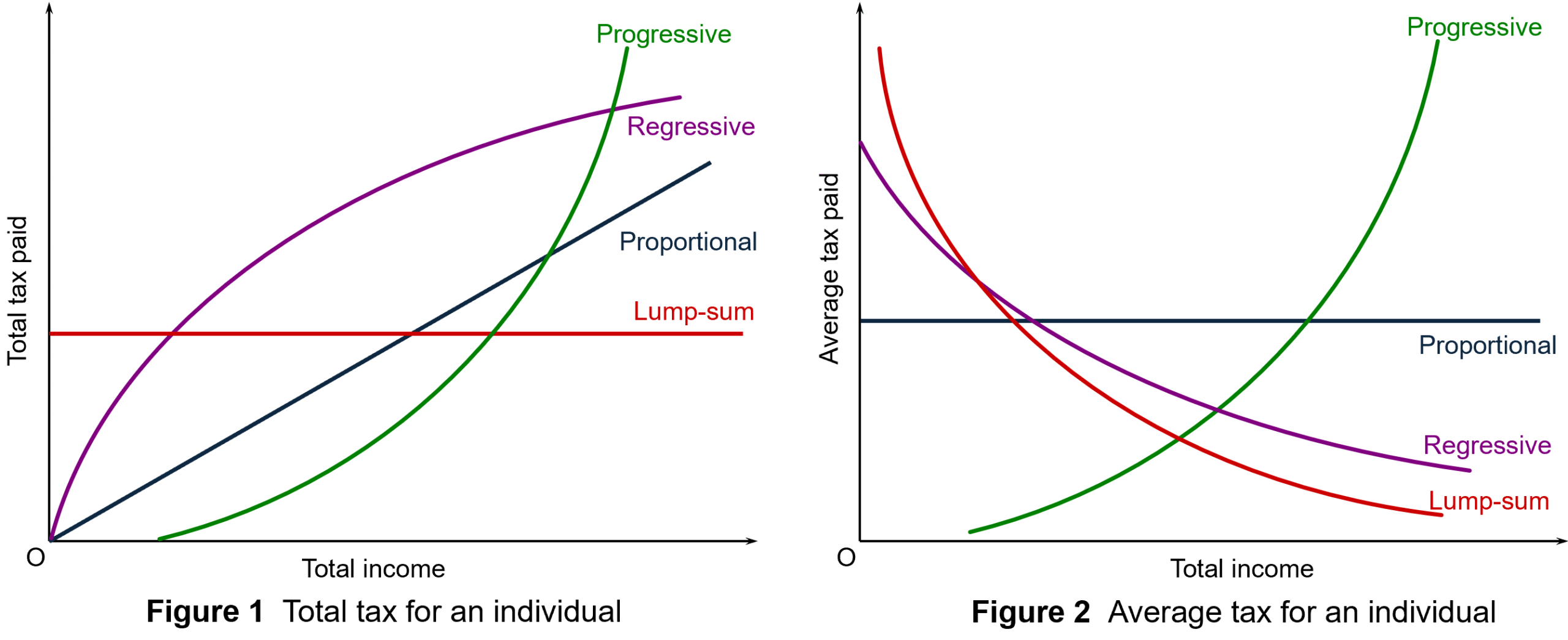
Figures 1 and 2 illustrate these different categories of tax: see Figure 11.12 in Economics, 12th edition. (Click here for a PowerPoint.) Income taxes in most countries are progressive, although just how progressive depends on the differences between the tax bands and the size of personal tax-free allowances. A flat-rate income tax with no allowances is shown by the black line in each diagram, the slope in Figure 1 and the height in Figure 2 depending on the tax rate.
Arguments for a flat-rate income tax
Generally, arguments in favour of flat-rate taxes come from the political right. The two main arguments in favour are tax simplification and incentives.
Advocates argue that a flat tax system makes tax collection easier and makes tax evasion harder. If there are no exemptions, then it can be easier to check that people are paying their taxes and working out the correct amount they owe. It is argued that, in contrast, high tax rates on top earners can encourage tax evasion.
Flat taxes can also be part of a drive to reduce the size of the informal economy. As the VoxEU article states:
Unlike progressive taxes, which include complex and numerous exceptions left to the tax collectors’ discretion, the flat tax is clear cut. In combination with the low rate, its simplicity considerably reduces the stimuli for being informal.
Several post-communist countries in Eastern Europe adopted flat taxes, but for most they were seen as a temporary measure to reduce the informal sector and clamp down on tax evasion. Most have now adopted progressive taxes, with the exceptions of Bulgaria and until recently Russia.
 The second major argument is that lower taxes for higher earners, especially for entrepreneurs, can act as a positive incentive. People work harder and there is more investment. The argument here is that the positive substitution effect from the lower tax (work is more profitable now and hence people substitute work for leisure) is greater than the negative income effect (lower taxes increase take-home pay so that people do not need to work so much now to maintain their standard of living).
The second major argument is that lower taxes for higher earners, especially for entrepreneurs, can act as a positive incentive. People work harder and there is more investment. The argument here is that the positive substitution effect from the lower tax (work is more profitable now and hence people substitute work for leisure) is greater than the negative income effect (lower taxes increase take-home pay so that people do not need to work so much now to maintain their standard of living).
Then there is the question of tax evasion. With high rates of income tax for top earners, such people may employ accountants to exploit tax loopholes and hide earnings. This could be seen as highly unfair by middle-income earners who are still paying relatively high rates of tax. Even though a move to flat taxes is likely to mean a cut in tax rates for high earners, the tax take from them could be higher. There is evidence that post-communist and developing countries that have adopted flat taxes have found an increase in tax revenues as evasion is harder.
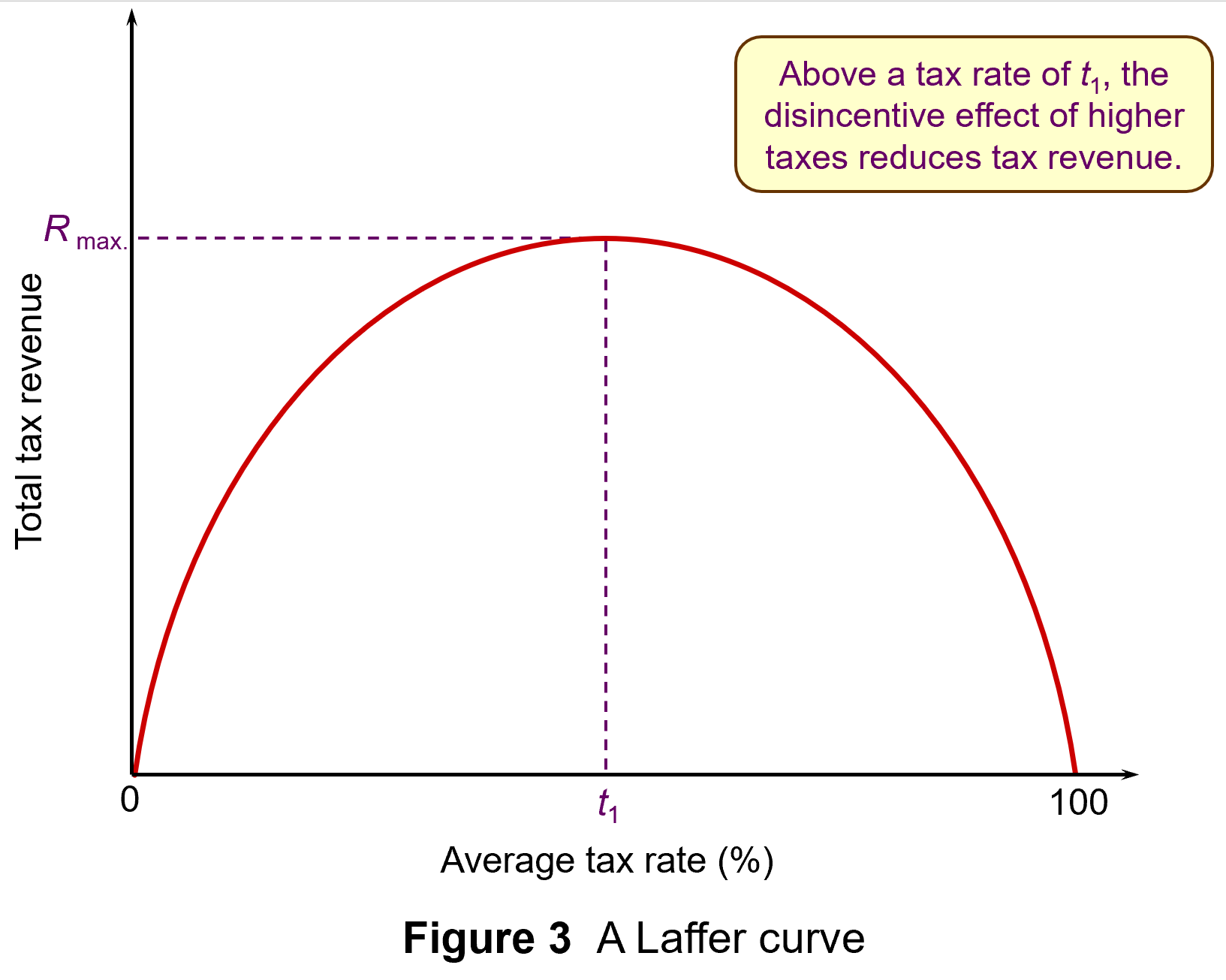 The Laffer curve is often used to illustrate such arguments that high top tax rates can lead to lower tax revenue. Professor Art Laffer was one of President Reagan’s advisers during his first administration (1981–4): see Box 11.3 in Economics, 11th edition. Laffer was a strong advocate of income tax cuts, arguing that substantial increases in output would result and that tax revenues could consequently increase.
The Laffer curve is often used to illustrate such arguments that high top tax rates can lead to lower tax revenue. Professor Art Laffer was one of President Reagan’s advisers during his first administration (1981–4): see Box 11.3 in Economics, 11th edition. Laffer was a strong advocate of income tax cuts, arguing that substantial increases in output would result and that tax revenues could consequently increase.
The Laffer curve in Figure 3 shows tax revenues increasing as the tax rate increases – but only up to a certain tax rate (t1). Thereafter, tax rates become so high that the resulting fall in output more than offsets the rise in tax rate. When the tax rate reaches 100 per cent, the revenue will once more fall to zero, since no one will bother to work. (Click here for a PowerPoint)
However, as Box 11.3 explains, evidence suggests that tax rates in most countries were well below t1 in the 1980s and certainly are now, given the cuts in income tax rates that have been made around the world over the past 20 years.
Arguments against flat-rate income taxes
 The main argument against moving from a progressive to a flat-rate income tax in an advanced country, such as the UK, is that is would involve a large-scale redistribution of income from the poor to the rich. If the tax were designed to raise the same amount of revenue as at present, those on low incomes would pay more tax than now, as their tax rate would rise to the new flat rate. Those on high incomes would pay less tax, as their marginal rate would fall to the new flat rate.
The main argument against moving from a progressive to a flat-rate income tax in an advanced country, such as the UK, is that is would involve a large-scale redistribution of income from the poor to the rich. If the tax were designed to raise the same amount of revenue as at present, those on low incomes would pay more tax than now, as their tax rate would rise to the new flat rate. Those on high incomes would pay less tax, as their marginal rate would fall to the new flat rate.
If a new flat-rate tax in the UK also replaced national insurance contributions (NICs), then the effect would be less extreme as NICs are currently initially progressive, as there is a personal allowance before the 8% rate is applied (on incomes above £12 570 in 2024/25). But above a higher NI threshold (£50 270 in 2024/25), the marginal rate drops to 2%, making it a regressive tax beyond that level. Figure 4 shows tax and NI rates in England, Wales and Northern Ireland for 2024/25. (Click here for a PowerPoint.)
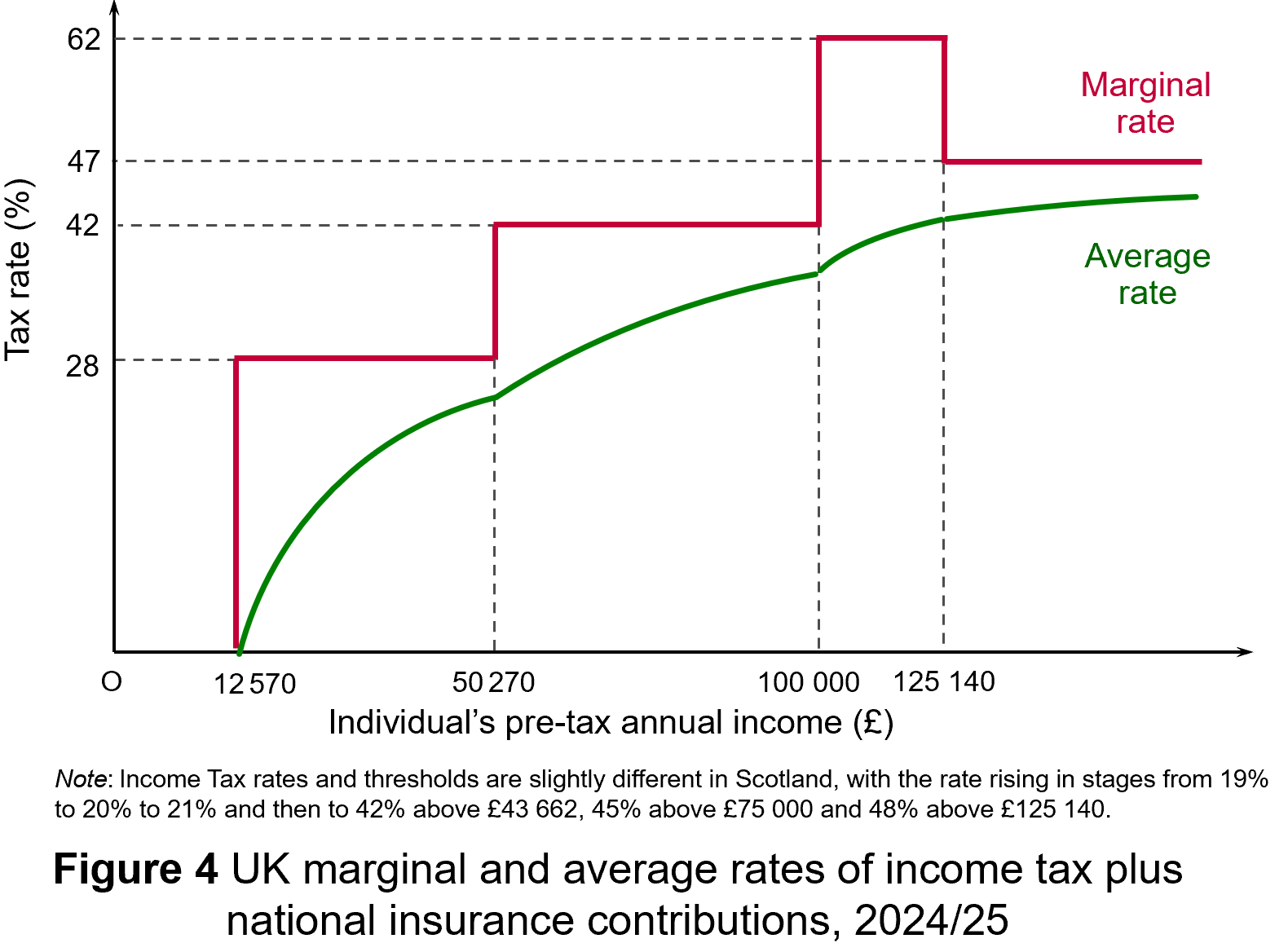 Nevertheless, even if a new flat-rate tax replaced NICs as well as varying rates of income tax, it would still involve a large-scale redistribution from low-income earners to high-income earners. The effect would be mitigated somewhat if personal allowances were raised so that the tax only applied to mid-to-higher incomes. Then the redistribution would be from middle-income earners to high-income earners and also somewhat to low-income earners: i.e. those below, or only a little above, the new higher personal allowance. If, on the other hand, personal allowances were scrapped so that the flat tax applied to all incomes, then there would be a massive redistribution from people on low incomes, including very low incomes, to those on high incomes.
Nevertheless, even if a new flat-rate tax replaced NICs as well as varying rates of income tax, it would still involve a large-scale redistribution from low-income earners to high-income earners. The effect would be mitigated somewhat if personal allowances were raised so that the tax only applied to mid-to-higher incomes. Then the redistribution would be from middle-income earners to high-income earners and also somewhat to low-income earners: i.e. those below, or only a little above, the new higher personal allowance. If, on the other hand, personal allowances were scrapped so that the flat tax applied to all incomes, then there would be a massive redistribution from people on low incomes, including very low incomes, to those on high incomes.
 One of the arguments used to justify a flat-rate tax is that its simplicity would ensure greater compliance. But in an advanced country, compliance is high, except, perhaps, for those on very high incomes. Most people in the UK and many other countries, have tax deducted automatically from their wages. People cannot avoid such taxes.
One of the arguments used to justify a flat-rate tax is that its simplicity would ensure greater compliance. But in an advanced country, compliance is high, except, perhaps, for those on very high incomes. Most people in the UK and many other countries, have tax deducted automatically from their wages. People cannot avoid such taxes.
As far as the self-employed are concerned, they file tax returns online and the software automatically works out the tax due. There are no complex calculations that have to be performed by the individual. There is come scope for tax evasion by charging various expenditures to the business that are really personal spending, but the tax authorities can ask for evidence and sometimes do, with penalties for false claims.
What tax evasion does take place, could still do so with a flat tax. At a rate of, say, 20%, it would still be financially beneficial for a dishonest person to lie if they could get way with it.
Conclusions
If the government did try to introduce a flat-rate income tax, there would probably be an outcry. Also, as some rich people would gain a very large amount of money, the number of people gaining would be lower than the number losing if the total revenue raised were to remain the same. In other words, it would be politically difficult to achieve if the number of losers exceeded the number of gainers.
It is true that if the top rate of income tax were very high, then reducing it might bring in more revenue. But at 45%, or 47% if you include NICs, the top marginal rate in the UK is relatively low compared with other countries. In 2024, the UK had the second lowest top rate of tax out of Western European countries (behind Norway and Switzerland) and only the 16th highest out of 33 European countries when Central and Eastern European countries are also included (see the final ink below under ‘Information’). Reducing the UK’s top rate would be unlikely to bring in more revenue and would redistribute income to high-income earners.
Articles
- Flat tax rate is an ‘attractive idea’, Kemi Badenoch says
The Guardian, Helena Horton (16/12/24)
- Tories could move to a system of ‘flat taxes’ where everyone pays the same rate, Kemi Badenoch indicates
Mail Online, Jason Groves (16/12/24)
- Flat Tax: What It Is and How It Works
Investopedia (8/11/24)
- Flat tax reform in Ukraine: Lessons from Bulgaria
VoxEU, Simeon Djankov (11/12/22)
- Why not… introduce a flat tax?
BBC News, Brian Wheeler (3/7/13)
- Five country cases illustrate how best to improve tax collection
IMF Finance and Development Magazine, Bernardin Akitoby (March 2018)
- Flat taxes and the desire to increase inequality
Funding the Future blog, Richard Murphy (15/5/14)
- Options for a UK ‘flat tax’: some simple simulations
IFS Briefing Note, Stuart Adam and James Browne (August 2006)
- Are the Flat Tax Folks Winning — or Have They Already Won?
Inequality.org, Sam Pizzigati (20/4/24)
Information
Questions
- Distinguish between progressive, proportional, regressive and lump-sum taxes. Into which of these four categories would you place (a) VAT, (b) motor fuel duties, (c) tobacco duties, (d) road-fund licence, (e) inheritance tax? Where the answer is either progressive or regressive, how progressive or regressive are they?
- What are the income and substitution effects of changing tax rates?
- Explain the Laffer curve and consider whether it is likely to be symmetrical.
- Discuss the desirability of having a flat tax set at a relatively high rate (say 25%) with tax-free personal allowances up to the level of income considered to be the poverty threshold. (In the UK the poverty threshold is often defined as 60% of median income.)
- In the London Palladium event where Kemi Badenoch stated that flat taxes were a very attractive idea, she also said that ‘We cannot afford flat taxes where we are now. We need to make sure we rewire our economy so that we can lighten the burden of tax and the regulation on individuals and on those businesses that are just starting out, in particular’. What do you think she meant by this?
- Find out what Bulgaria’s experience of a flat tax of 10% has been.
 In a blog from March 2023 (reproduced below), we saw how there has been growing pressure around the world for employers to move to a four-day week. Increasing numbers of companies have adopted the model of 80% of the hours for 100% of the pay.
In a blog from March 2023 (reproduced below), we saw how there has been growing pressure around the world for employers to move to a four-day week. Increasing numbers of companies have adopted the model of 80% of the hours for 100% of the pay. Since the financial crisis of 2007–8, the growth in UK productivity has been sluggish. This is illustrated in the chart, which looks at the production industries: i.e. it excludes services, where average productivity growth tends to be slower. The chart has been updated to 2024 Q2 – the latest data available. (Click here for a PowerPoint of the chart.)
Since the financial crisis of 2007–8, the growth in UK productivity has been sluggish. This is illustrated in the chart, which looks at the production industries: i.e. it excludes services, where average productivity growth tends to be slower. The chart has been updated to 2024 Q2 – the latest data available. (Click here for a PowerPoint of the chart.)  Productivity in the UK is lower than in many other competitor countries. According to the ONS, output per hour in the UK in 2021 was $59.14 in the UK. This compares with an average of $64.93 for the G7 countries, $66.75 in France, £68.30 in Germany, $74.84 in the USA, $84.46 in Norway and $128.21 in Ireland. It is lower, however, in Italy ($54.59), Canada ($53.97) and Japan ($47.28).
Productivity in the UK is lower than in many other competitor countries. According to the ONS, output per hour in the UK in 2021 was $59.14 in the UK. This compares with an average of $64.93 for the G7 countries, $66.75 in France, £68.30 in Germany, $74.84 in the USA, $84.46 in Norway and $128.21 in Ireland. It is lower, however, in Italy ($54.59), Canada ($53.97) and Japan ($47.28). The model adopted varied across companies, depending on what was seen as most suitable for them. Some gave everyone Friday off; others let staff choose which day to have off; others let staff work 80% of the hours on a flexible basis.
The model adopted varied across companies, depending on what was seen as most suitable for them. Some gave everyone Friday off; others let staff choose which day to have off; others let staff work 80% of the hours on a flexible basis. On the day he came to office, President Trump signed a series of executive orders. One of these was to set in motion the process of withdrawing from the UN Paris climate agreement. Section 3(a) of the order reads:
On the day he came to office, President Trump signed a series of executive orders. One of these was to set in motion the process of withdrawing from the UN Paris climate agreement. Section 3(a) of the order reads: Since 2020, each country has been required to submit its own emission-reduction targets, known as ‘nationally determined contributions’ (NDCs), and the actions it will take to meet them. Every five years each country must submit a new NDC more ambitious than the last.
Since 2020, each country has been required to submit its own emission-reduction targets, known as ‘nationally determined contributions’ (NDCs), and the actions it will take to meet them. Every five years each country must submit a new NDC more ambitious than the last. In April 2016 the USA signed the Paris Agreement. As stated above, the Paris Agreement came into effect on 4 November 2016.
In April 2016 the USA signed the Paris Agreement. As stated above, the Paris Agreement came into effect on 4 November 2016.  Climate change is directly caused by market failures. One of the most important of these is that the atmosphere is a common resource: it is not privately owned; it is a global ‘commons’. Individuals and firms use it at a zero price. If the price of any good or service to the user is zero, there is no incentive to economise on its use. Thus for the emitter there are no private costs of using the atmosphere in this way as a ‘dump’ for their emissions and, in a free market, no incentive to reduce the climate costs.
Climate change is directly caused by market failures. One of the most important of these is that the atmosphere is a common resource: it is not privately owned; it is a global ‘commons’. Individuals and firms use it at a zero price. If the price of any good or service to the user is zero, there is no incentive to economise on its use. Thus for the emitter there are no private costs of using the atmosphere in this way as a ‘dump’ for their emissions and, in a free market, no incentive to reduce the climate costs. These climate costs are external costs to the firm and are illustrated in the figure. It shows an industry that emits CO2. To keep the analysis simple, assume that it is a perfectly competitive industry with demand and supply given by curves D and S, which are equal to the marginal private benefits (MPB) and marginal private costs (MPC), respectively. There are no externalities on the demand side and hence MPB equals the marginal social cost (MSB). Market equilibrium is at point a, with output at Qpc and price at Ppc. (Click
These climate costs are external costs to the firm and are illustrated in the figure. It shows an industry that emits CO2. To keep the analysis simple, assume that it is a perfectly competitive industry with demand and supply given by curves D and S, which are equal to the marginal private benefits (MPB) and marginal private costs (MPC), respectively. There are no externalities on the demand side and hence MPB equals the marginal social cost (MSB). Market equilibrium is at point a, with output at Qpc and price at Ppc. (Click  In other words, other things being equal, the free market overproduces products with climate externalities. If the output is to be reduced to the social optimum of Q*, then the government will need to take measures such as those advocated in the Paris Agreement. These could include imposing taxes on products, such as electricity generated by fossil fuels, or on the emissions themselves. Or green alternatives, such as wind power, could be subsidised.
In other words, other things being equal, the free market overproduces products with climate externalities. If the output is to be reduced to the social optimum of Q*, then the government will need to take measures such as those advocated in the Paris Agreement. These could include imposing taxes on products, such as electricity generated by fossil fuels, or on the emissions themselves. Or green alternatives, such as wind power, could be subsidised. Withdrawal from the Paris Agreement and promoting fossil fuels will increase US emissions. Scientific consensus is that this will have a negative effect on climate change. Only part of these climate costs will be borne by the USA, although the severity of recent fires in California, fanned by strong Santa Ana winds, and more violent hurricanes are two examples of costs of climate change to the USA itself.
Withdrawal from the Paris Agreement and promoting fossil fuels will increase US emissions. Scientific consensus is that this will have a negative effect on climate change. Only part of these climate costs will be borne by the USA, although the severity of recent fires in California, fanned by strong Santa Ana winds, and more violent hurricanes are two examples of costs of climate change to the USA itself.
 The election of Donald Trump saw the market price of bitcoin rise from $67 839 on election day (5 November 2024) to £106 168 on 18 December: a rise of 56%. It was $104 441 the day before inauguration (20 January 2025).
The election of Donald Trump saw the market price of bitcoin rise from $67 839 on election day (5 November 2024) to £106 168 on 18 December: a rise of 56%. It was $104 441 the day before inauguration (20 January 2025). The supply of many cryptocurrencies is not controlled with the objective of achieving price stability. Indeed, certain cryptocurrencies, such as bitcoin (the coins with the highest total market value of approximately $2060bn) have a limited maximum supply. The supply of bitcoin in January 2025 is officially 19.81m, 94.3% of the eventual official total of 21m. However, with some 1.8m coins lost, the current effective total supply is more like 18m and the ceiling 19.2m. New coins are created by ‘mining’, involving massive computer power to perform complex calculations. Coins in circulation at any one time are therefore fixed and increase only slowly and at a decelerating rate over time, with increased mining costs per coin. On any one day, however, the supply offered for sale can fluctuate wildly.
The supply of many cryptocurrencies is not controlled with the objective of achieving price stability. Indeed, certain cryptocurrencies, such as bitcoin (the coins with the highest total market value of approximately $2060bn) have a limited maximum supply. The supply of bitcoin in January 2025 is officially 19.81m, 94.3% of the eventual official total of 21m. However, with some 1.8m coins lost, the current effective total supply is more like 18m and the ceiling 19.2m. New coins are created by ‘mining’, involving massive computer power to perform complex calculations. Coins in circulation at any one time are therefore fixed and increase only slowly and at a decelerating rate over time, with increased mining costs per coin. On any one day, however, the supply offered for sale can fluctuate wildly. There are some cryptocurrencies that are suitable as a medium of exchange and as a unit of value. These are ‘stablecoins’, whose value is linked 1:1 to a major currency, such as the US dollar or euro. Supply is adjusted to maintain this value. Stablecoins are used primarily for transactions. They account for some two-thirds of all transactions using crypto. They are particularly used for transactions in parts of the world with monetary instability and/or limited access to major currencies.
There are some cryptocurrencies that are suitable as a medium of exchange and as a unit of value. These are ‘stablecoins’, whose value is linked 1:1 to a major currency, such as the US dollar or euro. Supply is adjusted to maintain this value. Stablecoins are used primarily for transactions. They account for some two-thirds of all transactions using crypto. They are particularly used for transactions in parts of the world with monetary instability and/or limited access to major currencies.

 During the pandemic, most people who were not furloughed were forced to work from home. After lockdown restrictions were lifted, many employers decided to continue with people working remotely, at least for some of the time.
During the pandemic, most people who were not furloughed were forced to work from home. After lockdown restrictions were lifted, many employers decided to continue with people working remotely, at least for some of the time. Increasingly, however, employers who had introduced hybrid working are requiring their employees to return to the office, arguing that productivity and hence profits will rise as a result. Amazon is an example. Other employers, such as Asda, are increasing the time required in the office for hybrid workers.
Increasingly, however, employers who had introduced hybrid working are requiring their employees to return to the office, arguing that productivity and hence profits will rise as a result. Amazon is an example. Other employers, such as Asda, are increasing the time required in the office for hybrid workers. For employees, less time and money is spent on commuting, which accounts for nearly an hour’s worth of the average worker’s daily time. According to the ONS survey, respondents spent an additional 24 minutes per day on sleep and rest and 15 minutes on exercise, sports and other activities that improved well-being compared to those who worked on-site. Working at home can make juggling work and home life easier, especially when workers can work flexible hours during the day, allowing them to fit work around family commitments.
For employees, less time and money is spent on commuting, which accounts for nearly an hour’s worth of the average worker’s daily time. According to the ONS survey, respondents spent an additional 24 minutes per day on sleep and rest and 15 minutes on exercise, sports and other activities that improved well-being compared to those who worked on-site. Working at home can make juggling work and home life easier, especially when workers can work flexible hours during the day, allowing them to fit work around family commitments.  Some employers have found it hard to monitor and engage employees working from home. Workers may be easily distracted at home by other family members, especially if they don’t have a separate study/home office. People may feel detached from their co-workers on days they work from home. After a time, productivity may wane as workers find ways of minimising the amount of time actually working during declared work times.
Some employers have found it hard to monitor and engage employees working from home. Workers may be easily distracted at home by other family members, especially if they don’t have a separate study/home office. People may feel detached from their co-workers on days they work from home. After a time, productivity may wane as workers find ways of minimising the amount of time actually working during declared work times. Where work needs to be done in teams and where team meetings are an important element of that work, it would generally make sense for such meetings to be held in person, especially when there needs to be a lot of discussion. If the team requires a brief catch up, however, this may be more efficiently done online via Teams or Zoom.
Where work needs to be done in teams and where team meetings are an important element of that work, it would generally make sense for such meetings to be held in person, especially when there needs to be a lot of discussion. If the team requires a brief catch up, however, this may be more efficiently done online via Teams or Zoom.  At an event at the London Palladium on 6 December staged to protest against elements in the recent Budget, the Conservative leader, Kemi Badenoch, was asked whether she would introduce a flat-rate income tax if the Conservatives were returned to government. She replied that it was a very attractive idea. But first the economy would need ‘rewiring’ so that the tax burden could be lightened.
At an event at the London Palladium on 6 December staged to protest against elements in the recent Budget, the Conservative leader, Kemi Badenoch, was asked whether she would introduce a flat-rate income tax if the Conservatives were returned to government. She replied that it was a very attractive idea. But first the economy would need ‘rewiring’ so that the tax burden could be lightened.
 The second major argument is that lower taxes for higher earners, especially for entrepreneurs, can act as a positive incentive. People work harder and there is more investment. The argument here is that the positive substitution effect from the lower tax (work is more profitable now and hence people substitute work for leisure) is greater than the negative income effect (lower taxes increase take-home pay so that people do not need to work so much now to maintain their standard of living).
The second major argument is that lower taxes for higher earners, especially for entrepreneurs, can act as a positive incentive. People work harder and there is more investment. The argument here is that the positive substitution effect from the lower tax (work is more profitable now and hence people substitute work for leisure) is greater than the negative income effect (lower taxes increase take-home pay so that people do not need to work so much now to maintain their standard of living). The Laffer curve is often used to illustrate such arguments that high top tax rates can lead to lower tax revenue. Professor Art Laffer was one of President Reagan’s advisers during his first administration (1981–4): see Box 11.3 in Economics, 11th edition. Laffer was a strong advocate of income tax cuts, arguing that substantial increases in output would result and that tax revenues could consequently increase.
The Laffer curve is often used to illustrate such arguments that high top tax rates can lead to lower tax revenue. Professor Art Laffer was one of President Reagan’s advisers during his first administration (1981–4): see Box 11.3 in Economics, 11th edition. Laffer was a strong advocate of income tax cuts, arguing that substantial increases in output would result and that tax revenues could consequently increase.  The main argument against moving from a progressive to a flat-rate income tax in an advanced country, such as the UK, is that is would involve a large-scale redistribution of income from the poor to the rich. If the tax were designed to raise the same amount of revenue as at present, those on low incomes would pay more tax than now, as their tax rate would rise to the new flat rate. Those on high incomes would pay less tax, as their marginal rate would fall to the new flat rate.
The main argument against moving from a progressive to a flat-rate income tax in an advanced country, such as the UK, is that is would involve a large-scale redistribution of income from the poor to the rich. If the tax were designed to raise the same amount of revenue as at present, those on low incomes would pay more tax than now, as their tax rate would rise to the new flat rate. Those on high incomes would pay less tax, as their marginal rate would fall to the new flat rate. Nevertheless, even if a new flat-rate tax replaced NICs as well as varying rates of income tax, it would still involve a large-scale redistribution from low-income earners to high-income earners. The effect would be mitigated somewhat if personal allowances were raised so that the tax only applied to mid-to-higher incomes. Then the redistribution would be from middle-income earners to high-income earners and also somewhat to low-income earners: i.e. those below, or only a little above, the new higher personal allowance. If, on the other hand, personal allowances were scrapped so that the flat tax applied to all incomes, then there would be a massive redistribution from people on low incomes, including very low incomes, to those on high incomes.
Nevertheless, even if a new flat-rate tax replaced NICs as well as varying rates of income tax, it would still involve a large-scale redistribution from low-income earners to high-income earners. The effect would be mitigated somewhat if personal allowances were raised so that the tax only applied to mid-to-higher incomes. Then the redistribution would be from middle-income earners to high-income earners and also somewhat to low-income earners: i.e. those below, or only a little above, the new higher personal allowance. If, on the other hand, personal allowances were scrapped so that the flat tax applied to all incomes, then there would be a massive redistribution from people on low incomes, including very low incomes, to those on high incomes. One of the arguments used to justify a flat-rate tax is that its simplicity would ensure greater compliance. But in an advanced country, compliance is high, except, perhaps, for those on very high incomes. Most people in the UK and many other countries, have tax deducted automatically from their wages. People cannot avoid such taxes.
One of the arguments used to justify a flat-rate tax is that its simplicity would ensure greater compliance. But in an advanced country, compliance is high, except, perhaps, for those on very high incomes. Most people in the UK and many other countries, have tax deducted automatically from their wages. People cannot avoid such taxes.